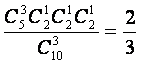
三、解答题

20.(本小题满分12分)

    袋中装着标有数字1，2，3，4，5的小球各2个．从袋中任取3个小球，

按3个小球上最大数字的9倍计分，每个小球被取出的可能性都相等，

用ξ表示取出的3个小球上的最大数字，求：

    (Ⅰ)取出的3个小球上的数字互不相同的概率；

    (Ⅱ)随机变量ξ的概率分布和数学期望；

    (Ⅲ)计分介于20分到40分之间的概率．

解：(Ⅰ)解法一：“一次取出的3个小球上的数字互不相同”的事件记为A，

        则P(A)=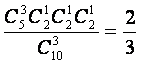

        解法二：“一次取出的3个小球上的数字互不相同”的事件记为A，

“一次取出的3个小球上有两个数字相同”的事件记为B，

则事件A和事件B是互斥事件，因为

P（B）＝

        所以P(A)＝1-P(B)＝1-＝.

    (Ⅱ)由题意，ξ有可能的取值为：2，3，4，5．

    P(ξ=2)=；

    P(ξ=3)=；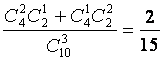

    P(ξ=4)=；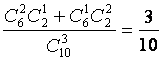

    P（ξ=5）=.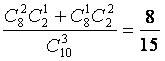

所以随机变量ξ的概率分布为

    因此ξ的数学期望为

Eξ＝2×+3×+4×+5×=.

（Ⅲ）“一次取球所得计分介于20分到40分之间”的事件记为C，则

      P(C)＝P(“ξ=3”或“ξ=4”)=P(“ξ=3”)+P(“ξ=4”)=