一、选择题(每题5分)

（3）双曲线mx²+y²=1的虚轴长是实轴长的2倍，则m=( )

（A）    （B）-4    （C）4     （D）

（8）抛物线y=-x²上的点到直线的距离的最小值是(  )

（A）     （B）     （C）     （D）3

（9）设平面向量a₁，a₂，a₃的和a₁+a₂+a₃=0.如果平面各量b₁，b₂，b₃满足

│b_i│=2│a_i│，且a_i的顺时针旋转后与b_i同向，其中i-1，2，3，则( )

（A）-b₁+b₂+b₃=0      （B）b₁-b₂+b₃=0

（C）b₁+b₂-b₃=0       （D）b₁+b₂+b₃=0

（20）（本小题满分12分）

在平面直角坐标系xOy中，有一个以和为焦点、离心率为的

椭圆，设椭圆在第一象限的部分为曲线C，动点P在C上，C在点P处的切线与x、y轴的

交点分别为A、B，且向量，求：

（Ⅰ）点M的轨迹方程；

（Ⅱ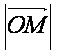）的最小值。