三、解答题

20．（本小题满分12分）

已知等差数列的前项和为，．

（1）求的值；

（2）若与的等差中项为，满足，求数列的前项和．

   本小题考查数列的概念，等差数列，等比数列，对数与指数互相转化等基

础知识，考查综合运用数学知识解决问题的能力,满分12分.

（Ⅰ）解法一：当n=1时，a₁=S₁=p-2+q，

当n≥2时，a_n=S_n-S_n-1=pn²-2n+q-p（n-1）²+2（n-1）-q

             =2pn-p-2.

∵{a_n}是等差数列，

∴p-2+q=2p-p-2.

∴q=0.

解法二：当n=1时，a₁=S₁=p-2+q，

当n≥2时，a_n=S_n-S_n-1=pn²-2n+q-p（n-1）²+2（n-1）-q

             =2pn-p-2.

当n≥3时，a_n-a_n-1=2pn-p-2-［2p（n-1）-p-2］=2p，

a₂=p-2+q+2p=3p-2+q，

又a₂=2p·2-P-2=3P-2，

所以3p-2+q=3p-2，得

q=0.

（Ⅱ）解：∵a₃=，

∴a₃=18.

又a₃=6p-p-2，

∴6p-p-2=18.

∴p=4.

∴a_n=8n-6.

又a_n=2log₂h_n，得

b_n=2^4a-3，

∴b₁=2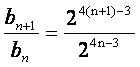，=2⁴=16，即

{b_n}是等比数列.

所以数列{b_n}的前n项和T_n=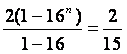（16ⁿ-1）.