，
.求:三、解答题
(17) (本小题满分12分)
已知函数，.求:
( = 1 \* ROMAN I)
函数
的最大值及取得最大值的自变量
的集合；
( = 2 \* ROMAN II)
函数的单调增区间.
本小题考查三角公式、三角函数的性质及已知三角函数值求角等基础知识，
考查综合运用三角函数有关知识的能力.满分12分.
(Ⅰ)解法一：∵f（x）=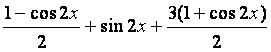
=2+sin2x+cos2x
=2+
sin（2x+
）
∴当2x+
=2kπ+
，即x=kπ+
（k∈Z）时,f（x）取得最大值2+
.
因此f（x）取得最大值的自变量x的集合是{x|x=kπ+
，k∈Z}.
解法二：∵f（x）=（sin2x·cos2x）+ sin2x +2cos2x
=1+sin2x+1+cos2x
=2+
sin（2x+
）.
∴当2x+=2kπ+
，即x=kπ+
（k∈Z）时f（x）取得最大值2+
.
因此,f（x）取得最大值的自变量x的集合是{x|x=kπ+
，（k∈Z}.
(Ⅱ)解：f（x）=2+sin（2x+）,
由题意得2kπ-≤2x+
≤2kπ+
（k∈Z）.即
kπ-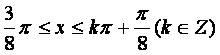
.
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。