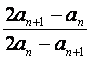三、解答题

22．(本小题满分14分)

    已知各项均为正数的数列{a_n}满足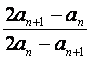=a_na_n+1，n∈N^*．

    (1)求数列{a_n}的通项公式；

(2)设S_n=a²₁+a²₂+…+a²_n，T_n=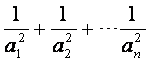，求S_n+T_n，并确定最小正整数

n，使S_n+T_n为整数．

   解(1)条件式化为a_n+1-

因此{a_n-}为一个等比数列，其公比为2，首项为a₁-.

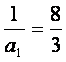所以a_n-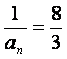·2^n-1=(n∈N*)…………①

因a_n＞0,由①解出a_n=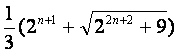…………②

（2）由①有S_n+T_n=

                =

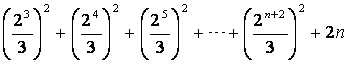
                =(4ⁿ-1)+2n(n∈N^*)

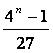为使S_n+T_n=(4ⁿ-1)+2n为整数，当且仅当为整数.

当n=1,2时，显然S_n+T_n不为整数，

当n≥3时，∵4ⁿ-1=(1+3)ⁿ-1=C·3+ C·3²+3³（C+…+3^n-3C）

∴只需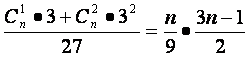为整数，

∵3n-1与3互质，∴n为9的整数倍.

当n=9时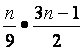，=13为整数.

故n的最小正整数为9.