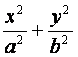三、解答题

21．(本小题满分12分)

如图，椭圆Q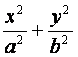：=1(a＞b＞0)的右焦点为F(c，0)，过点F的一动直线m

绕点F转动，并且交椭圆于A、B两点，P为线段AB的中点．

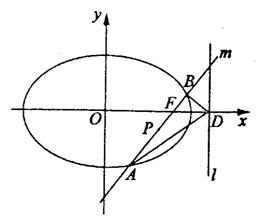
    (1)求点P的轨迹H的方程；

    (2)若在Q的方程中，令a²=1+cosθ+sinθ,b²=sinθ(0＜θ≤).

    设轨迹H的最高点和最低点分别为M和N.当θ为何值时，△MNF为—个正三角形?

    解：如图，

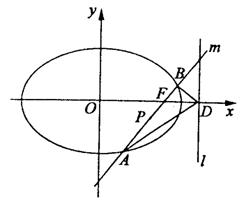
（1）设椭圆Q：=1上的点A（x₁,y₁）、B（x₂,y₂），又设P点坐标为

P（x,y），则

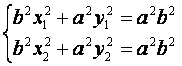
由①-②得

b²(x₁-x₂)2x+a²(y₁-y₂)2y=0.

1°当AB不垂直x轴时，x₁≠x₂

得到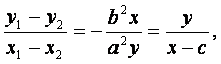化简得：

b²x²+a²y²-b²cx=0……（*）

2°当AB垂直于x轴时，点P即为点F，满足方程（*）

所以点P的轨迹H的方程为：b²x²+a²y²-b²cx=0

（2）因为轨迹H的方程可化为：

∴M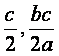（），N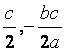（），F(c,0),使△MNF为一个正三角形时，

则tan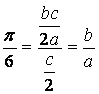,即a²=3b².由于a²=1+cosθ+sinθ,b²=sinθ(0＜θ≤),

则1+cosθ+sinθ=3sinθ,得θ=2arctan(或表示为θ=arctan).