一、选择题(每题5分)
2.已知向量![]() =(2,t),
=(2,t),![]() =(1,2),若t=t1时,
=(1,2),若t=t1时,![]() ∥
∥![]() ;t=t2时,
;t=t2时,![]() ⊥
⊥![]() ,则( )
,则( )
A.t1=-4,t2=-1 B.t1=-4,t2=1
C.t1=4,t2=-1 D.t1=4, t2=1
7.圆x2+y2-4x-4y-10=0上的点到直线x+y-14=0的最大距离与最小距离的差是( )
A.36
B.18 C.6![]() D.5
D.5![]()
9.过双曲线M:x2-![]() =1的左顶点A作斜率为l的直线l,若l与双曲线M的两条渐近线
=1的左顶点A作斜率为l的直线l,若l与双曲线M的两条渐近线
分别相交于点B、C,且|AB|=|BC|,则双曲线M的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
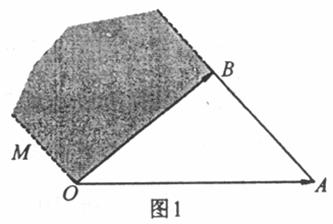
10.如图1,OM∥AB,点P在由射线OM、线段OB及AB的延长线围成的阴影区域内(不含
边界),且![]() ,则实数对(x,y)可以是(
)
,则实数对(x,y)可以是(
)
A.(![]() )
B.(
)
B.( )
)
C.(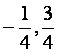 )
D.(
)
D.(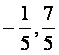 )
)
三、解答题
21.(本小题满分14分)
已知椭圆C1∶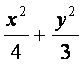 =1,抛物线C2∶(y-m)2=2px(p>0),且C1、C2的公共弦AB
=1,抛物线C2∶(y-m)2=2px(p>0),且C1、C2的公共弦AB
过椭圆C1的右焦点.
(Ⅰ)当AB⊥x轴时,求p、m的值,并判断抛物线C2的焦点是否在直线AB上;
(Ⅱ)若P=![]() 且抛物线C2的焦点在直线AB上,求m的值及AB的方程.
且抛物线C2的焦点在直线AB上,求m的值及AB的方程.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。