三、解答题

18．(本小题满分14分)

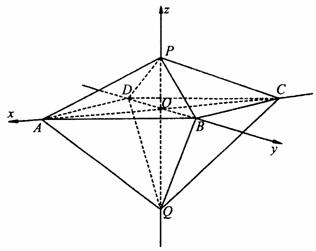
    如图4，己知两个正四棱锥P-ABCD与Q-ABCD的高分别为1和2，AB=4．

    (Ⅰ)证明PQ⊥平面ABCD；

    (Ⅱ)求异面直线AQ与PB所成的角；

    (Ⅲ)求点P到平面QAD的距离．  

        解法一  (Ⅰ)连结AC、BD，设AC∩BD=O.因为P-ABCD与Q-ABCD都是正四

棱锥，

所以PO⊥平面ABCD，QO⊥平面ABCD．从而P、O、Q三点在一条直线上，所

以PQ⊥平面ABCD．

(Ⅱ)由题设知，ABCD是正方形，所以AC⊥BD．

由(Ⅰ)，PQ⊥平面ABCD，故可分别以直线CA、DB、QP为x轴、y轴、z轴建立

空间直角坐标系(如图)，由题设条件，相关各点的坐标分别是P(0，0，1)，

A(2，0，0)，Q(0，0，-2)，B(0，2，0)．

所以=(-2，0，-2)，=(0，2，-1).

于是cos＜，＞=．

从而异面直线AQ与PB所成的角是arccos．

(Ⅲ)由(Ⅱ)，点D的坐标是(0，-2，0)，=(-2，-2，0)，

=(0，0，-3)，

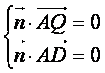设=(x，y,z)是平面QAD的一个法向量,由得．

取x=1，得=(1，-1，-)．

所以点P到平面QAD的距离d=．

解法二  (Ⅰ)取AD的中点M，连结PM，QM．

因为P-ABCD与Q-ABCD都是正四棱锥，所以AD⊥PM，AD⊥QM.

从而AD⊥平面PQM．又PQ平面PQM，所以PQ⊥AD．

同理PQ⊥AB，所以PQ⊥平面ABCD．

(Ⅱ)连结AC、BD，设AC∩BD=O，由PQ⊥平面ABCD及正四棱锥的性质可知O

在PQ上，从而P、A、Q、C四点共面．

取OC的中点N，连结PN.

因为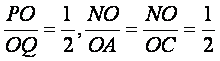，所以，从而AQ∥PN，∠BPN(或其补

角)是异面直线AQ与PB所成的角．

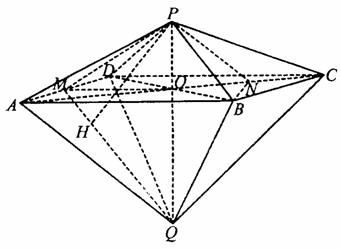
连结BN.

因为PB==3，

PN=，

BN=，

所以cos∠BPN=.

从而异面直线AQ与PB所成的角是arccos.

(Ⅲ)由(Ⅰ)知，AD⊥平面PQM，所以平面QAD⊥平面PQM．

过P作PH⊥QM于H，则PH⊥平面QAD，所以PH的长为点P到平面QAD的距离．

连结OM，因为OM=AB=2=OQ，所以∠MQP=45°．

又PQ=PO+QO=3，于是PH=PQsin45°=．

即点P到平面QAD的距离是．