16．（本小题满分12分）

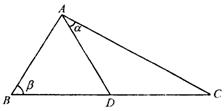
如图3，D是直角△ABC斜边BC上一点，AB=AD，记∠CAD=α，∠ABC=β.

（Ⅰ）证明：sinα+cos2β=0；

（Ⅱ）若AC=DC，求β的值.

解  （Ⅰ）如图，因为α=-∠BAD=-（π-2β）=2β-，

所以 sinα=sin（2β-）=-cos2β，

即sinα+cos2β=0.

（Ⅱ）在△ADC中，由正弦定理得，即.

所以sinβ=sinα.

由（Ⅰ），sinα=-cos2β，所以sinβ=-cos2β=-（1-2sin²β）.

即2sin²β-sinβ-=0.

解得sinβ=或sinβ=-.

因为0＜β＜，所以sinβ=，从而β=.