 =1(a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
=1(a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,三、解答题
21.(本小题满分14分)
设A、B分别为椭圆 =1(a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
=1(a,b>0)的左、右顶点,椭圆长半轴的长等于焦距,
且x=4是它的右准线。
(Ⅰ)求椭圆的方程;
(Ⅱ)设P为右准线上不同于点(4,0)的任意一点,若直线AB,BP分别与椭圆相交于
异于A,B的M、N,证明点B在以MN为直径的圆内.
本小题主要考查直线、圆和椭圆等平面解析几何的基础知识,考查综合运用数学知识进行推理运算的能力和解决问题的能力。
解:(Ⅰ)依题意得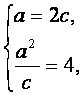 解得
解得 从而
从而![]() ,故椭圆方程为
,故椭圆方程为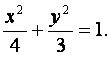
(Ⅱ)解法1:由(Ⅰ)得A(-2,0),B(2,0),设M![]() ,
,![]() M点在椭圆上,
M点在椭圆上, ①,又M点异于顶点A、B,
①,又M点异于顶点A、B,![]() 由P、A、M三点共线可
由P、A、M三点共线可
得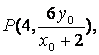 从而
从而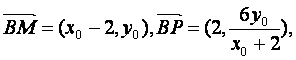
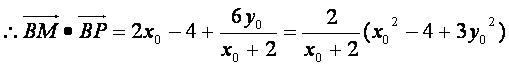 ②.将①式代入②式化简得
②.将①式代入②式化简得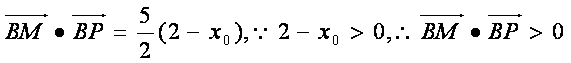 ,于是
,于是![]() 为锐角,
为锐角,
从而![]() 为钝角,故点
为钝角,故点![]() 在以
在以![]() 为直径的圆内.
为直径的圆内.
解法2:由(Ⅰ)得A(-2,0),B(2,0),设P![]() M
M![]() ,N
,N![]() ,则直线AP的
,则直线AP的
方程为 ,直线BP的方程为.
,直线BP的方程为.![]()
![]() 点M、N分别在直线AP、BP上,
点M、N分别在直线AP、BP上,
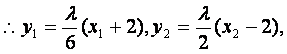 从而
从而 .③
.③
联立 消去
消去![]() 得
得![]()
![]() 是方程的两要,
是方程的两要, 即
即
又![]() ⑤
⑤
于是由③、④式代入⑤式化简可得
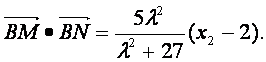
![]() 点在椭圆上,且异于顶点
点在椭圆上,且异于顶点![]()
又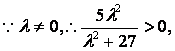 从而
从而![]()
故![]() 为钝角,即点
为钝角,即点![]() 在以
在以![]() 为直径的圆内,
为直径的圆内,
解法3:由(Ⅰ)得![]() 设
设![]() 则
则![]() ,
,
又![]() 的中点
的中点![]() 的坐标为
的坐标为
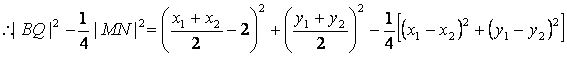 ,化简得
,化简得 ,直线
,直线![]() 的方程为
的方程为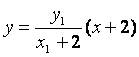 ,直线
,直线![]() 的
的
方程为 .
.
![]() 点
点![]() 在准线
在准线![]() 上,
上,
 即
即 ⑦
⑦
又∵![]() 点在椭圆上,
点在椭圆上, 即
即![]()
于是将⑦、⑧式代入⑥式化简可得
从而![]() 在以
在以![]() 为直径的圆内,
为直径的圆内,
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。