三、解答题

19．（本小题满分10分）

在某校举行的数学竞赛中，全体参赛学生的竞赛成绩近似服从正态分布N（70，100）。

已知成绩在90分以上（含90分）的学生有12名。

（Ⅰ）试问此次参赛的学生总数约为多少人？

（Ⅱ）若该校计划奖励竞赛成绩排在前50名的学生，试问设奖的分数线约为多少分？

可供查阅的（部分）标准正态分布表（x₀）=P(x＜x₀）

19．本小题主要考查正态分布、对立事件的概念和标准正态分布表的查阅，

考查运用概率统计知识解决实际问题的能力。

解：（Ⅰ）设参赛学生的分数为,因为（70，100），由条件知，

P（）=1-P(）=1-F（90）=1-

这说明成绩在90分以上（含90分）的学生人数约占全体参赛人数的2.28%。

因此，参赛的人数约为

（Ⅱ）假定设奖的分数线为X分，则

P（

即查表得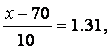解得x=83.1.

故设奖的分数线约为83分。