三、解答题

18．（本小题满分12分）

   如图，在棱长为1的正方体ABCD—A₁B₁C₁D₁中，P是侧棱CC₁上的一点，CP=m。

（Ⅰ）试确定m，使得直线AP与平面BDD₁B₁所成角的正切值为；

（Ⅱ）在线段A₁C₁上是否存在一个定点Q，使得对任意的m，D₁Q在平面APD₁上的射影

垂直于AP，并证明你的结论。

    本小题主要考查线面关系，直线与平面所成角的有关知识及空间想象能力和

推理运算能力，考查应用向量知识解决数学问题的能力。

解法1：（Ⅰ）连AC，设ACBD=O，AP与面BDD₁B₁交于点G，连结OG。

因为PC//面BDD₁B₁，面BDD₁B₁面APC=OG，故OG∥PC，所以。

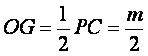    又AO⊥DB，AO⊥BB₁，所以AO⊥面BDD₁B₁。

    故∠AGO即为AP与面BDD₁B₁所成的角。

在。

故当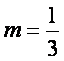时，直线AP与平面BDD₁B₁所成角的正切值为3。

（Ⅱ）依题意，要在A₁C₁上找一点Q，使得D₁Q⊥AP。

可推测A₁C₁的重点Q₁即为所求的Q点。

因为D₁O₁⊥A₁C₁,D₁O₁⊥AA₁,所以D₁O₁⊥面ACC₁A₁。

又AP面ACC₁A₁，故D₁O₁⊥AP。

从而D₁O₁在平面AD₁P上的射影与AP垂直

解法2：（1）建立如图所示的空间直角坐标系，则A（1，0，0），B（1，1，0）

，P（0，1，m）,C(0,1,0),D(0,0,0),(1,1,1),D(0,0,1)。

所以（-1，-1，0），。

又由向量。

设AP与平面BB₁D₁D所成的角为，则sin=cos()

  =

依题意有。

故当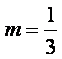时，直线AP与平面BD D₁B₁所成角的正切值为3。

（Ⅱ）若在A₁C₁上存在这样的点Q，设此点的横坐标为x.

则Q（x,1－x,1），

依题意，对任意的m要使在平面APD₁上的射影垂直于AP，等价于⊥AP即Q为的中点时，满足题设要求。