三、解答题
(19)(本小题满分13分)
如图,在四棱锥![]() 中,
中,![]() 底面
底面![]() ,
,![]() 为直角,
为直角,![]()
![]() ,
,![]() 、
、![]() 分别为
分别为![]() 、CD的中点。
、CD的中点。
(Ⅰ)试证:![]() 平面
平面![]() ;
;
(Ⅱ)设PA=K·AB,且二面角![]() 的平面角大于
的平面角大于![]() ,求
,求![]() 的取值范围。
的取值范围。
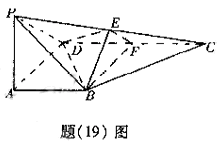
解法一:
(I)证:由已知![]()
![]()
![]() 且
且![]() 为直角,故
为直角,故![]() 是矩形,从而
是矩形,从而![]() ,
,
又![]() 底面
底面![]() ,
,![]() ,故由三垂线定理知
,故由三垂线定理知![]() ,在
,在![]() 中,
中,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,故
的中点,故![]()
![]()
![]() ,从而
,从而![]() ,
,
由此得![]() 面
面![]() .
.
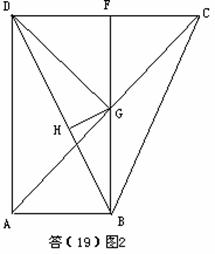
(II)连接AC交BF于G,易知G为AC的中点,连接EG,则在![]() 中易知
中易知
EG![]() PA,又因PA
PA,又因PA![]() 底面ABCD,故EG
底面ABCD,故EG![]() 底面ABCD,在底面ABCD中,过G作
底面ABCD,在底面ABCD中,过G作
GH![]() BD,垂足为H,连接EH,由三垂线定理知EH
BD,垂足为H,连接EH,由三垂线定理知EH![]() BD,从而
BD,从而![]() 为二面
为二面
角E-BD-C的平面角。
设![]() ,则在
,则在![]() 中,有
中,有
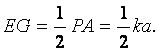
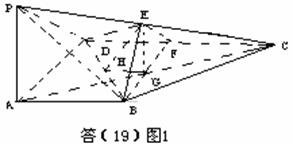
以下计算![]() ,考虑底面的平面图(如答(19)图2)。连接
,考虑底面的平面图(如答(19)图2)。连接![]() ,
,
因
故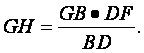
在![]() 中,因
中,因![]() 得
得![]() 而
而![]()
从而得
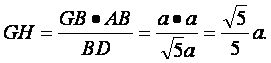
因此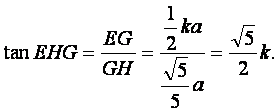
由![]() 知
知![]() 是锐角,故要使
是锐角,故要使![]() ,必须
,必须
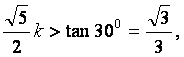
解之得,![]() 的取值范围为
的取值范围为
解法二:
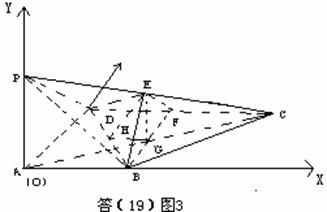
(I)如图,以![]() 为原点,
为原点,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 所在直线为y轴,
所在直线为y轴,![]() 所在
所在
直线为![]() 轴建立,空间直角坐标系,设
轴建立,空间直角坐标系,设![]() ,则易知点
,则易知点![]()
![]() 的
的
坐标分别为

从而![]()
![]() 故
故![]()
设![]() 则
则![]() 而
而![]() 为
为![]() 中点,故
中点,故
![]()
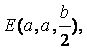 从而
从而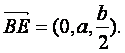
![]() 故
故![]()
由此得![]() 面
面![]() .
.
(II)设![]() 在
在![]() 平面上的射影为
平面上的射影为![]() ,过
,过![]() 作
作![]() 垂足为
垂足为![]() ,
,
由三垂线定理知![]() ,从而
,从而![]() 为二面角
为二面角![]() 的平面角。
的平面角。
由![]() 得
得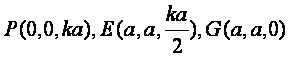 ,
,
设![]() ,则
,则![]() ,
,
由![]() 得
得![]() ,即
,即
![]() ①
①
又因![]() ,且
,且![]() 与
与![]() 的方向相同,故
的方向相同,故 ,即
,即
![]() ②
②
由①②解得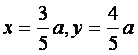 ,从而
,从而 ,
,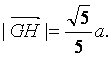
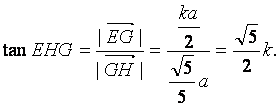
由![]() 知
知![]() 是锐角,由
是锐角,由![]() ,得
,得![]() ,即
,即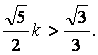
故![]() 的取值范围为
的取值范围为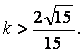
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。