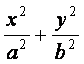三、解答题

(19)(本小题共14分)

椭圆C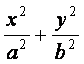：=1(a＞b＞0)的两个焦点为F₁，F₂，点P在椭圆C上，且

PF₁⊥F₁F₂，|PF₁|=，|PF₂|=.

(Ⅰ)求椭圆C的方程；

(Ⅱ)若直线l过圆x²+y²+4x-2y=0的圆心M，交椭圆C于A，B两点，且A，B

关于点M对称，求直线l的方程.

解法一：

(Ⅰ)因为点P在椭圆C上，所以2a=|PF₁|+|PF₂|=6，a=3.

在Rt△PF₁F₂中，|F₁F₂|==2，故椭圆的半焦距c=，

从而b²=a²-c²=4，

所以椭圆C的方程为.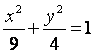

(Ⅱ)设A，B的坐标分别为(x₁，y₁)，(x₂，y₂).

已知圆的方程为(x+2)²+(y-1)²=5，所以圆心M的坐标为(-2，1)，

从而可设直线l的方程为

y=k(x+2)+1，

代入椭圆C的方程得

(4+9k²)x²+(36k²+18k)x+36k²+36k-27=0.

因为A，B关于点M对称，

所以= -2，

解得k=，

所以直线l的方程为y=(x+2)+1，

即8x-9y+25=0.

(经检验，所求直线方程符合题意.)

解法二：

(Ⅰ)同解法一.

(Ⅱ)已知圆的方程为(x+2)²+(y-1)²=5，所以圆心M的坐标为(-2，1).设A，B

的坐标分别为(x₁，y₁)，(x₂，y₂).由题意x₁≠x₂且

，                               ①

.                                 ②

由①-②得

=0.       ③

因为A，B关于点M对称，

所以x₁+x₂= -4，y₁+y₂=2，

代入③得，

即直线l的斜率为，

所以直线l的方程为y-1=(x+2)，

即8x-9y+25=0.

(经检验，所求直线方程符合题意.)

(20)(共14分)

解：(Ⅰ)由S₁₄=98得2a₁+13d=14，

又a₁₁=a₁+10d=0，

故解得d=-2，a₁=20.

因此，{a_n}的通项公式是a_n=22-2n，n=1，2，3，….

(Ⅱ)由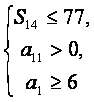得

即

由①+②得-7d＜11，

即d＞-.

由①+③得13d≤-1，

即d≤-.

于是-＜d≤-.

又d∈Z，故

d=-1.                                                          ④

将④代入①②得10＜a₁≤12.

又a₁∈Z，故a₁=11或a₁=12.

所以，所有可能的数列{a_n}的通项公式是

a_n=12-n和a_n=13-n，n=1，2，3，….