三、解答题

（17）（本小题共14分）

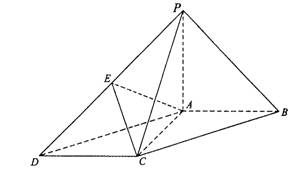
如图，在底面为平行四边形的四棱锥P-ABCD中，AB⊥AC，PA⊥平面ABCD，

且PA=AB，点E是PD的中点.

（Ⅰ）求证：AC⊥PB；

（Ⅱ）求证：PB∥平面AEC；

（Ⅲ）求二面角E-AC-B的大小.

解法一：

（Ⅰ）∵PA⊥平面ABCD，

∴AB是PB在平面ABCD上的射影.

又∵AB⊥AC，AC平面ABCD，

∴AC⊥PB.

（Ⅱ）连接BD，与AC相交于O，连接EO.

          ∵ABCD是平行四边形，

          ∴O是BD的中点，

          又E是PD的中点，

          ∴EO∥PB.

          又PB平面AEC，EO平面AEC，

          ∴PB∥平面AEC.

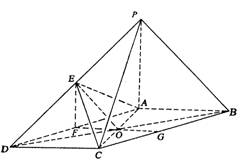
（Ⅲ）过O作FG∥AB，交AD于F，交BC于G，则F为AD的中点.

          ∵AB⊥AC，

          ∴OG⊥AC，

          又由（Ⅰ），（Ⅱ）知，AC⊥PB，EO∥PB，

          ∴AC⊥EO.

          ∴∠EOG是二面角E-AC-B的平面角.

          连接EF，在△EFO中，

          EF=PA，FO=AB，又PA=AB，EF⊥PO，

          ∴ ∠EOF=45°，∠EOG=135°，

           ∴二面角E-AC-B的大小为135°.

   解法二：

（Ⅰ）建立空间直角坐标系A-xyz，如图.

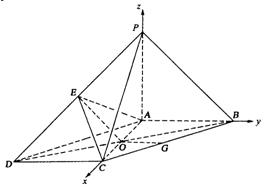
     设AC=a，PA=b，则有A（0,0,0），B（0,b,0），C（a,0,0），P（0,0,b），

           ∴

           ∴AC⊥PB.

（Ⅱ）连接BD，与AC相交于O，连接EO.

      由已知得D（a，-b，0），

      E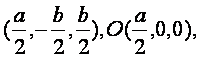

      ∴

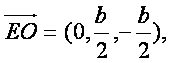
      又

      ∴

      ∴PB∥EO，

      又PB平面AEC，EO平面AEO，

      ∴PB∥平面AEC.

（Ⅲ）取BC中点G，连接OG，则点G的坐标为（），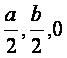

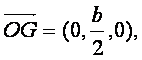
      又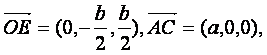

      ∴

      ∴OE⊥AC，OG⊥AC，

      ∴∠EOG是二面角E-AC-B的平面角.

      ∵cosEOG=cos＜,＞=

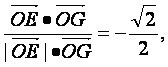
      ∴∠EOG=135°,

      ∴二面角E-AC-B的大小为135°.