解答题
(21)(本小题满分14分)
已知mÎR,设P:![]() 和
和![]() 是方程
是方程![]() 的两个实根,不等式
的两个实根,不等式
![]() 对任意实数
对任意实数![]() Î[-1,1]恒成立;
Î[-1,1]恒成立;
Q:函数 在(-¥,+¥)上有极值
在(-¥,+¥)上有极值![]()
求使P正确且Q正确的m的取值范围![]()
解:(Ⅰ)由题设![]() 和
和![]() 是方程
是方程![]() 的两个实根,得
的两个实根,得
![]() +
+![]() =
=![]() 且
且![]()
![]() =-2,
=-2,
所以,
当![]() Î[-1,1]时,
Î[-1,1]时,![]() 的最大值为9,即
的最大值为9,即![]() £3
£3![]()
由题意,不等式![]() 对任意实数
对任意实数![]() Î[1,1]恒成立的m的解集
Î[1,1]恒成立的m的解集
等于不等式![]() 的解集
的解集![]() 由此不等式得
由此不等式得
![]() ①
①
或 ![]() ②
②
不等式①的解为![]()
![]()
不等式②的解为![]() 或
或![]()
![]()
因为,对![]() 或
或![]() 或
或![]() 时,P是正确的
时,P是正确的![]()
(Ⅱ)对函数 求导
求导
令![]() ,即
,即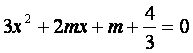
![]() 此一元二次不等式的判别式
此一元二次不等式的判别式

![]()
若D=0,则![]() 有两个相等的实根
有两个相等的实根![]() ,且
,且![]() 的符号如下:
的符号如下:
|
|
(-¥, |
|
( |
|
|
+ |
0 |
+ |
因为,f(![]() )不是函数f(
)不是函数f(![]() )的极值
)的极值![]()
若D>0,则![]() 有两个不相等的实根
有两个不相等的实根![]() 和
和![]() (
(![]() <
<![]() ),且
),且![]() 的符号如下:
的符号如下:
|
x |
(-¥, |
|
( |
|
( |
|
|
+ |
0 |
- |
0 |
+ |
因此,函数f(![]() )在
)在![]() =
=![]() 处取得极大值,在
处取得极大值,在![]() =
=![]() 处取得极小值
处取得极小值![]()
综上所述,当且仅当D>0时,函数f(![]() )在(-¥,+¥)上有极值
)在(-¥,+¥)上有极值![]()
由![]() 得
得![]() 或
或![]() ,
,
因为,当![]() 或
或![]() 时,Q是正确得
时,Q是正确得![]()
综上,使P正确且Q正确时,实数m的取值范围为(-¥,1)È![]()
![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。