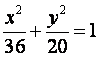解答题

19.点A、B分别是椭圆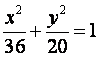长轴的左、右焦点，点F是椭圆的右焦点点P在椭圆上，

且位于x轴上方，

（1）求P点的坐标；

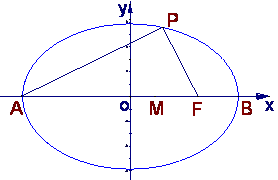    （2）设M是椭圆长轴AB上的一点，M到直线AP的

     距离等于，求椭圆上的点到点M的距离d的最小值

 [解]（1）由已知可得点A(－6,0),F(0,4)

   设点P(x,y),则={x+6,y},={x－4,y},

由已知可得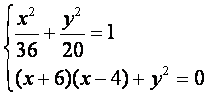　　　

    则2x2+9x－18=0,解得x=或x=－6.

   由于y>0,只能x=,于是y=.

   ∴点P的坐标是(,)

   (2) 直线AP的方程是x－y+6=0.

   设点M(m,0),则M到直线AP的距离是.

   于是=,又－6≤m≤6,解得m=2.

   椭圆上的点(x,y)到点M的距离d有

   d2=(x－2)2+y2=x－4x2+4+20－x2=(x－)2+15,

由于－6≤m≤6, ∴当x=时,d取得最小值