解答题
21.(本小题满分14分)
设![]() .
.![]() 两点在抛物线
两点在抛物线![]() 上,
上,![]() 是
是![]() 的垂直平分线
的垂直平分线![]()
1)当且仅当![]() 取何值时,直线
取何值时,直线![]() 经过抛物线的焦点
经过抛物线的焦点![]() ?证明你的结论;
?证明你的结论;
2)当直线![]() 的斜率为2时,求
的斜率为2时,求![]() 在
在![]() 轴上截距的取值范围
轴上截距的取值范围![]()
本小题主要考察直线与抛物线等基础知识,考察逻辑推理能力和综合分析、
解决问题的能力![]()
解法一:(1)![]()
![]() 、
、![]() 两点到抛物线的准线的距离相等
两点到抛物线的准线的距离相等
因为:抛物线的准线是![]() 轴的平行线,
轴的平行线,![]()
![]() ,依题意
,依题意![]() 、
、![]() 不同时为0
不同时为0
所以,上述条件等价于![]() ;
;
注意到:![]() ,所以上述条件等价于
,所以上述条件等价于![]()
![]()
即:当且仅当![]() 时,直线
时,直线![]() 经过抛物线的焦点
经过抛物线的焦点![]()
![]()
(2)设![]() 在
在![]() 轴上的截距为
轴上的截距为![]() ,依题意得
,依题意得![]() 的方程为
的方程为![]() ;过点
;过点![]() 、
、![]()
的直线方程可写为 ,所以
,所以![]() 、
、![]() 满足方程
满足方程 ,
,
即
![]() 、
、![]() 为抛物线上不同的两点等价于上述方程的判别式
为抛物线上不同的两点等价于上述方程的判别式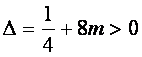 ,也就是:
,也就是:

![]() 设
设![]() 的中点
的中点![]() 的坐标为为
的坐标为为![]() ,则有:
,则有:
 ,
,
由![]() 得:
得: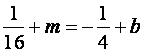 ,于是:
,于是: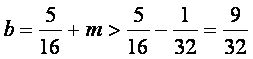
![]()
即:![]() 在
在![]() 轴上截距的取值范围是
轴上截距的取值范围是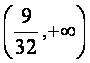
![]()
.解法二:(Ⅰ)∵抛物线![]() ,即
,即 ,
,
∴焦点为 …………………………………………1分
…………………………………………1分
(1)直线![]() 的斜率不存在时,显然有
的斜率不存在时,显然有![]() ………………3分
………………3分
(2)直线![]() 的斜率存在时,设为k, 截距为b
的斜率存在时,设为k, 截距为b
即直线![]() :y=kx+b
由已知得:
:y=kx+b
由已知得:
 ……5分
……5分
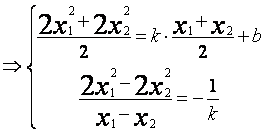
 ………7分
………7分 

即![]() 的斜率存在时,不可能经过焦点
的斜率存在时,不可能经过焦点 ……………………8分
……………………8分
所以当且仅当![]() =0时,直线
=0时,直线![]() 经过抛物线的焦点F……………9分
经过抛物线的焦点F……………9分
(II)解:设直线![]() 的方程为:y=2x+b,
的方程为:y=2x+b,
故有过AB的直线的方程为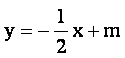 ,代入抛物线方程有2x2+
,代入抛物线方程有2x2+ =0,
得x1+x2=-
=0,
得x1+x2=-![]() .
.
由A.B是抛物线上不同的两点,于是上述方程的判别式 ,即
,即
由直线AB的中点为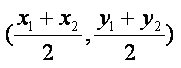 =
= ,
,
则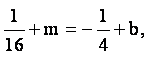 于是
于是
即得l在y轴上的截距的取值范围是
![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。