解答题
22.(本小题满分12分)
已知函数f(x)=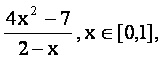
(1)求函数f(x)的单调区间和值域;
(2)设a≥1, 函数g(x)=x3-3a2x-2a, x∈[0,1], 若对于任意x1∈[0,1],
总存在x0∈[0,1],
使得g((x0)
=f(x1)成立,求a的取值范围![]()
解:
(1)对函数f(x)=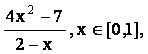 求导,得f’(x)=
求导,得f’(x)=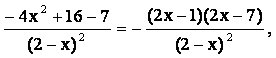 ,
,
令f’(x)=0解得x=![]() 或x=
或x=![]() .
当x变化时,f’(x), f(x)的变化情况如下表所示:
.
当x变化时,f’(x), f(x)的变化情况如下表所示:
|
x |
0 |
(0, |
|
|
1 |
|
f’(x) |
|
- |
0 |
+ |
|
|
f(x) |
|
↘ |
-4 |
↗ |
-3 |
所以,当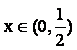 时,f(x)是减函数;当
时,f(x)是减函数;当 时,f(x)是增函数
时,f(x)是增函数![]()
当![]() 时,f(x)的值域是[-4,-3]
时,f(x)的值域是[-4,-3]![]()
(II)对函数g(x)求导,则g’(x)=3(x2-a2).
因为![]() ,当
,当![]() 时,g’(x)<5(1-a2)≤0,
时,g’(x)<5(1-a2)≤0,
因此当![]() 时,g(x)为减函数,
时,g(x)为减函数,
从而当x∈[0,1]时有g(x)∈[g(1),g(0)],
又g(1)=1-2a-3a2,g(0)=-2a,
即当x∈[0,1]时有g(x)∈[1-2a-3a2,-2a],
任给x1∈[0,1],f(x1)∈[-4,-3],存在x0∈[0,1]使得g(x0)=f(x1),
则[1-2a-3a2,-2a]![]() ,
,
即
![]() ,
,
解①式得a≥1或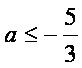 ,
,
解②式得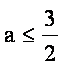 ,
,
又![]() ,故a的取值范围内是
,故a的取值范围内是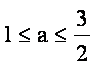 .
.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。