 的左、右焦点分别是F1(-c,0)、F2(c,0),
的左、右焦点分别是F1(-c,0)、F2(c,0),解答题
21.(本小题满分14分)
已知椭圆 的左、右焦点分别是F1(-c,0)、F2(c,0),
的左、右焦点分别是F1(-c,0)、F2(c,0),
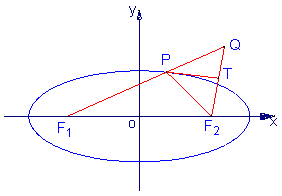
Q是椭圆外的动点,满足![]() 点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,
点P是线段F1Q与该椭圆的交点,点T在线段F2Q上,
并且满足![]()
 (Ⅰ)设
(Ⅰ)设![]() 为点P的横坐标,证明
为点P的横坐标,证明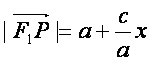 ;
;
(Ⅱ)求点T的轨迹C的方程;
(Ⅲ)试问:在点T的轨迹C上,是否存在点M,
使△F1MF2的面积S=![]() 若存在,求∠F1MF2
若存在,求∠F1MF2
的正切值;若不存在,请说明理由.
本小题主要考查平面向量的概率,椭圆的定义、标准方程和有关性质,轨迹的求法和应
用,以及综合运用数学知识解决问题的能力.满分14分.
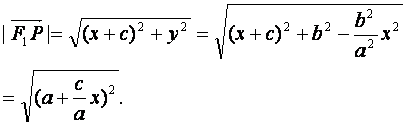
 (Ⅰ)证法一:设点P的坐标为
(Ⅰ)证法一:设点P的坐标为![]()
由P![]() 在椭圆上,得
在椭圆上,得
由 ,所以
,所以  ………………………3分
………………………3分
证法二:设点P的坐标为![]() 记
记![]()
则![]()
由
证法三:设点P的坐标为![]() 椭圆的左准线方程为
椭圆的左准线方程为
由椭圆第二定义得 ,即
,即
由 ,所以
,所以 …………3分
…………3分
(Ⅱ)解法一:设点T的坐标为![]()
当![]() 时,点(
时,点(![]() ,0)和点(-
,0)和点(-![]() ,0)在轨迹上.
,0)在轨迹上.
当|![]() 时,由
时,由![]() ,得
,得![]() .
.
又![]() ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
在△QF1F2中, ,所以有
,所以有![]()
综上所述,点T的轨迹C的方程是![]() …………………………7分
…………………………7分
解法二:设点T的坐标为![]() 当
当![]() 时,点(
时,点(![]() ,0)和点(-
,0)和点(-![]() ,0)在轨迹上.
,0)在轨迹上.
当|![]() 时,由
时,由![]() ,得
,得![]() .
.
又![]() ,所以T为线段F2Q的中点.
,所以T为线段F2Q的中点.
设点Q的坐标为(![]() ),则
),则
因此 ①
①
由![]() 得
得![]() ②
②
将①代入②,可得![]()
综上所述,点T的轨迹C的方程是![]() ……………………7分
……………………7分
(Ⅲ)解法一:C上存在点M(![]() )使S=
)使S=![]() 的充要条件是
的充要条件是

由③得![]() ,由④得
,由④得 所以,当
所以,当![]() 时,存在点M,使S=
时,存在点M,使S=![]() ;
;
当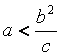 时,不存在满足条件的点M.………………………11分
时,不存在满足条件的点M.………………………11分
当 时,
时,![]() ,
,
由![]() ,
,
![]() ,
,
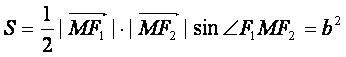 ,得
,得![]()
解法二:C上存在点M(![]() )使S=
)使S=![]() 的充要条件是
的充要条件是



由④得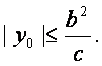 上式代入③得
上式代入③得
于是,当![]() 时,存在点M,使S=
时,存在点M,使S=![]() ;
;
当![]() 时,不存在满足条件的点M.………………………11分
时,不存在满足条件的点M.………………………11分
当 时,记
时,记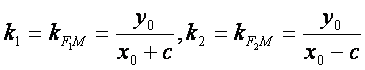 ,
,
由![]() 知
知![]() ,所以
,所以 ……14分
……14分
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。