解答题

19．（本小题满分14分）

已知椭圆C：＋＝1（a＞b＞0）的左．右焦点为F1、F2，离心率为e.

直线l：y＝ex＋a与x轴．y轴分别交于点A、B，M是直线l与椭圆C的一个公

共点，P是点F1关于直线l的对称点，设＝λ.

   （Ⅰ）证明：λ＝1－e2；

   （Ⅱ）确定λ的值，使得△PF1F2是等腰三角形.

（Ⅰ）证法一：因为A、B分别是直线l：与x轴、y轴的交点，

所以A、B的坐标分别是

.

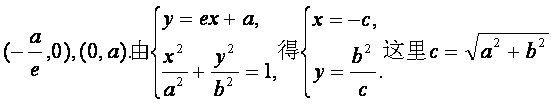所以点M的坐标是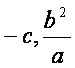（）.由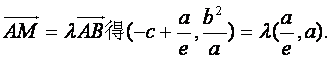

即

    证法二：因为A、B分别是直线l：与x轴、y轴的交点，

所以A、B的坐标分别是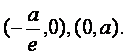设M的坐标是

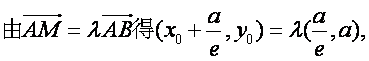
所以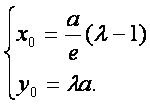     

因为点M在椭圆上，所以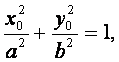 

即

解得

   （Ⅱ）解法一：因为PF1⊥l，所以∠PF1F2=90°+∠BAF1为钝角，

要使△PF1F2为等腰三角形，必有|PF1|=|F1F2|，即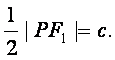

    设点F1到l的距离为d，

由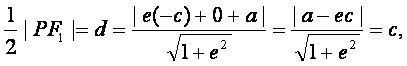

    得  

所以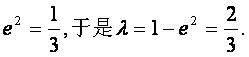

    即当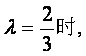△PF1F­2­­为等腰三角形.

解法二：因为PF1⊥l，所以∠PF1F2=90°+∠BAF1为钝角，要使

△PF1F2为等腰三角形，必有|PF1|=|F1F2|，

设点P的坐标是，

则，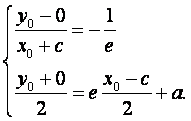

由|PF1|=|F1F2|得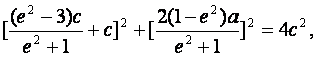

两边同时除以4a2，化简得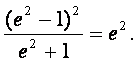 

从而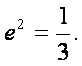

于是  

即当时，△PF1F2为等腰三角形