解答题
21.(本小题满分14分)
已知函数f(x)=lnx,g(x)=![]() ax2+bx,a≠0
ax2+bx,a≠0![]()
(Ⅰ)若b=2,且h(x)=f(x)-g(x)存在单调递减区间,求a的取值范围;
(Ⅱ)设函数f(x)的图象C1与函数g(x)图象C2交于点P、Q,过线段PQ的中
点作x轴的垂线分别交C1,C2于点M、N,证明C1在点M处的切线与C2在点N
处的切线不平行![]()
解:(I) ,
,
则
因为函数h(x)存在单调递减区间,所以![]() <0有解
<0有解![]()
又因为x>0时,则ax2+2x-1>0有x>0的解.
①当a>0时,y=ax2+2x-1为开口向上的抛物线,ax2+2x-1>0总有x>0的解;
②当a<0时,y=ax2+2x-1为开口向下的抛物线,而ax2+2x-1>0总有x>0的解;
则△=4+4a>0,且方程ax2+2x-1=0至少有一正根.此时,-1<a<0.
综上所述,a的取值范围为(-1,0)∪(0,+∞)![]()
(II)证法一 设点P、Q的坐标分别是(x1, y1),(x2, y2),0<x1<x2.
则点M、N的横坐标为
C1在点M处的切线斜率为
C2在点N处的切线斜率为
假设C1在点M处的切线与C2在点N处的切线平行,则k1=k2.
即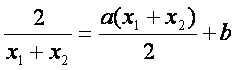 ,则
,则
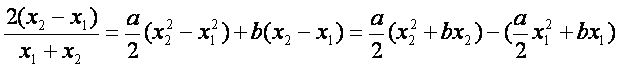
=![]()
所以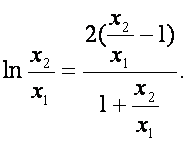 设
设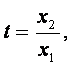 则
则 ①
①
令 则
则
因为![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() )上单调递增.
故
)上单调递增.
故![]()
则 .
这与①矛盾,假设不成立
.
这与①矛盾,假设不成立![]()
故C1在点M处的切线与C2在点N处的切线不平行![]()
证法二:同证法一得![]()
因为![]() ,所以
,所以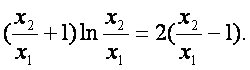
令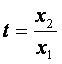 ,得
,得![]() ②
②
令
因为 ,所以
,所以![]() 时,
时,
故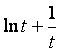 在[1,+
在[1,+![]() 上单调递增.从而
上单调递增.从而 ,即
,即![]()
于是![]() 在[1,+
在[1,+![]() 上单调递增
上单调递增![]()
故![]() 即
即![]() 这与②矛盾,假设不成立
这与②矛盾,假设不成立![]()
故C1在点M处的切线与C2在点N处的切线不平行![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。