解答题
21.(本小题满分12分)
设A、B是椭圆![]() 上的两点,点N(1,3)是线段AB的中点,线段AB的
上的两点,点N(1,3)是线段AB的中点,线段AB的
垂直平分线与椭圆相交于C、D两点![]()
(Ⅰ)确定![]() 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的![]() ,使得A、B、C、D四点在同一个圆上?并说明理由
,使得A、B、C、D四点在同一个圆上?并说明理由![]()
解:
(Ⅰ)解法一:依题意,可设直线AB的方程为y=k(x-1)+3,
代入![]() ,整理得:
,整理得:
![]()
![]() ①
①
设A(![]() ),B(
),B(![]() ),则
),则![]() ,
,![]() 是方程①的两个不同的根,
是方程①的两个不同的根,
∴![]() ,②
,②
且
![]() 由N(1,3)是线段AB的中点,得
由N(1,3)是线段AB的中点,得![]() =2,
=2,
∴![]()
![]() 解得k=-1,代入②得
解得k=-1,代入②得![]() ,
,
即![]() 的取值范围是(12,+∞)
的取值范围是(12,+∞)![]()
于是直线AB的方程为![]() ,即
,即![]()
![]()
解法二:设A(![]() ),B(
),B(![]() ),则有
),则有

![]()
依题意,
![]()
∵N(1,3)是AB的中点,∴![]() =2,
=2,![]() =6,从而
=6,从而![]()
![]()
又由N(1,3)在椭圆内,∴![]() ,
,
∴![]() 的取值范围是(12,+∞)
的取值范围是(12,+∞)![]()
直线AB的方程为![]() ,即
,即![]()
![]()
(Ⅱ)解法一:∵CD垂直平分AB,
∴直线CD的方程为y-3=x-1,即x-y+2=0![]() 代入椭圆方程,整理得
代入椭圆方程,整理得
![]()
![]() ③
③
又设C(![]() ),D(
),D(![]() ),CD的中点为M(
),CD的中点为M(![]() ),
),
则![]() ,
,![]() 是方程③的两根,
是方程③的两根,
∴![]() +
+![]() =-1,且
=-1,且 ,即M(
,即M(![]() ,
,![]() )
)![]()
于是由弦长公式可得
![]() ④
④
将直线AB的方程![]() 代入椭圆方程得
代入椭圆方程得
![]()
![]() ⑤
⑤
同理可得![]()
![]() ⑥
⑥
∵当![]() 时,
时,![]() >
>![]() ,
,
∴|AB|<|CD|![]()
假设存在![]() ,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心
,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心![]()
点M到直线AB的距离为

![]() ⑦
⑦
于是,由④⑥⑦式及勾股定理可得
![]()

故当![]() 时,A、B、C、D四点均在以M为圆心,|
时,A、B、C、D四点均在以M为圆心,|![]() |为半径的圆上
|为半径的圆上![]()
(注:上述解法中最后一步可按如下解法获得:
A、B、C、D共圆![]() ACD为直角三角形,A为直角
ACD为直角三角形,A为直角
![]()
![]() ,
,
即
![]() ⑧
⑧
由⑥式知,⑧式左边=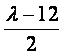 ,
,
由④⑦知,⑧式右边=

![]()
∴⑧式成立,即A、B、C、D四点共圆![]() )
)
解法二:由(Ⅱ)解法一知![]() ,
,
∵CD垂直平分AB,
∴直线CD的方程为y-3=x-1,代入椭圆方程,整理得
![]()
![]() ③
③
将直线AB的方程![]() 代入椭圆方程整理得
代入椭圆方程整理得
![]()
![]() ⑤
⑤
解③和⑤式可得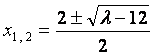 ,
, ,
,
不妨设A(![]() ,
, ),
),
C( ,
, ),D(
),D( ,
, )
)![]()
∴ ,
,
 ,
,
计算可得![]() ,
,
∴A在以CD为直径的圆上![]()
又B为A关于CD的对称点,
∴A、B、C、D四点共圆![]()
(注:也可用勾股定理证明AC⊥AD)
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。