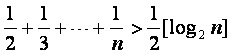 ,其中n为大于2的整数,
,其中n为大于2的整数,解答题
22.(本小题满分14分)
已知不等式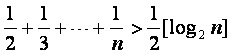 ,其中n为大于2的整数,
,其中n为大于2的整数,![]() 表示
表示
不超过![]() 的最大整数
的最大整数![]() 设数列{
设数列{![]() }的各项为正,且满足
}的各项为正,且满足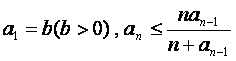 ,
,
![]()
![]()
(Ⅰ)证明: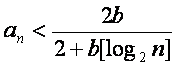 ,
,![]() ;
;
(Ⅱ)猜测数列{![]() }是否有极限?如果有,写出极限的值;
}是否有极限?如果有,写出极限的值;
(Ⅲ)试确定一个正整数N,使得当n>N时,对任意b>0,都有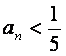
![]()
解:
(Ⅰ)证法一:∵当n≥2时,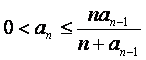 ,
,
∴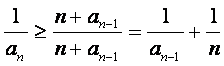 ,即
,即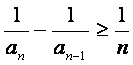 ,
,
于是有 ,
,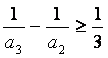 ,…,
,…,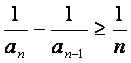 ,
,
所有不等式两边相加可得 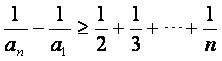
![]()
由已知不等式知,当n≥3时有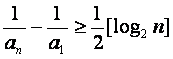
![]()
∵![]() ,∴
,∴
![]()
∴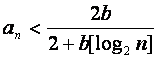
![]()
证法二:设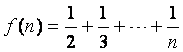 ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式
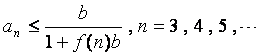
![]()
(ⅰ)当n=3时,由 ,
,
知不等式成立![]()
(ⅱ)假设当n=k(k≥3)时,不等式成立,即 ,则
,则
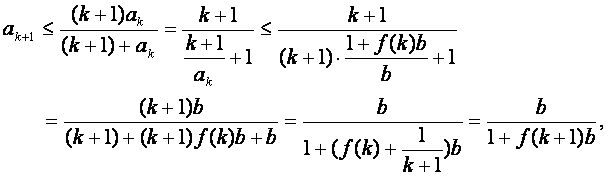
即当n=k+1时,不等式也成立![]()
由(ⅰ)(ⅱ)知,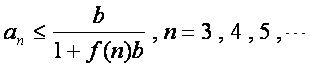
![]()
又由已知不等式得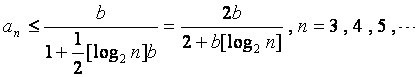
![]()
(Ⅱ)有极限,且![]()
![]()
(Ⅲ)∵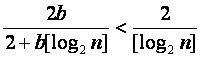 ,令
,令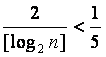 ,
,
则有![]() ,
,
故取N=1024,可使沁n>N时,都有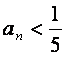
![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。