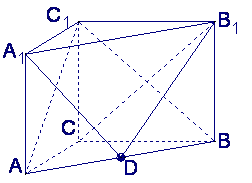
 如图, 在直三棱柱
如图, 在直三棱柱解答题
(16)(本小题共14分)
 如图, 在直三棱柱
如图, 在直三棱柱![]() 中,
中,![]() ,
,
点![]() 为
为![]() 的中点
的中点![]()
(Ⅰ)求证![]() ;
;
(Ⅱ)
求证![]() ;
;
(Ⅲ)求异面直线![]() 与
与![]() 所成角的余弦值
所成角的余弦值![]()
解:
(I)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4AB=5,
∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1;
(II)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,
∴ DE//AC1,
∵ DE![]() 平面CDB1,AC1
平面CDB1,AC1![]() 平面CDB1,∴
AC1//平面CDB1;
平面CDB1,∴
AC1//平面CDB1;
(III)∵ DE//AC1,∴ ∠CED为AC1与B1C所成的角,
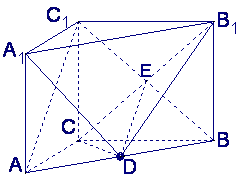 在△CED中,ED=
在△CED中,ED=![]() AC
1=
AC
1=![]() ,CD=
,CD=![]() AB=
AB=![]() ,CE=
,CE=![]() CB1=2
CB1=2![]() ,
,
∴ 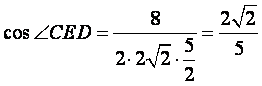 ,
,
∴ 异面直线 AC1与 B1C所成角的余弦值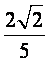 .
.
解法二:
∵直三棱锥![]() 底面三边长
底面三边长![]() ,
,
![]() 两两垂直
两两垂直![]()
如图建立坐标系,则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4),D(![]() ,2,0)
,2,0)
(Ⅰ)![]() ,
,![]()
![]()
(Ⅱ)设![]() 与
与![]() 的交点为E,则E(0,2,2)
的交点为E,则E(0,2,2)

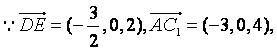
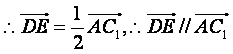
![]()
![]()
![]()
(Ⅲ)![]()
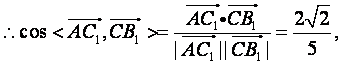
∴异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]()
![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。