解答题

(20)(本小题共14分)

     如图,直线与直线之间的阴影区域(不含边界)记为,

     其左半部分记为,右半部分记为

      (Ⅰ)分别有不等式组表示和

      (Ⅱ)若区域中的动点到的距离

     之积等于,求点的轨迹的方程;

      (Ⅲ)设不过原点的直线与(Ⅱ)中的曲线

     相交于两点,且与分别交于两点.

     求证△的重心与△的重心重合

解：（I）W1={(x, y)| kx<y<－kx, x<0}，W2={(x, y)|－kx<y<kx, x>0}，

    （II）直线l1：kx－y＝0，直线l2：kx＋y＝0，由题意得

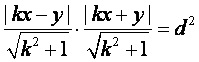    , 即，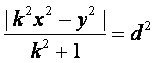

    由P(x, y)∈W，知k2x2－y2>0，

    所以 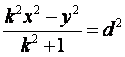，即,

    所以动点P的轨迹C的方程为；

  （III）当直线与x轴垂直时，可设直线的方程为x＝a（a≠0）．

   由于直线，曲线C关于x轴对称，且1与2关于x轴对称，于是M1M2，M3M4

   的中点坐标都为（a，0），所以△OM1M2，△OM3M4的重心坐标都为（a，0），

   即它们的重心重合，

    当直线1与x轴不垂直时，设直线的方程为y=mx+n（n≠0）

    由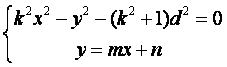，得

    由直线与曲线C有两个不同交点，可知k2－m2≠0且

   △=>0

   设M1，M2的坐标分别为(x1, y1)，(x2, y2)，

   则, ,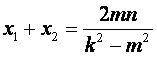

   设M3，M4的坐标分别为(x3, y3)，(x4, y4)，

   由得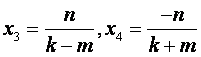

   从而，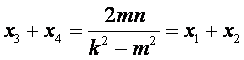

   所以y3+y4=m(x3+x4)+2n＝m(x1+x2)+2n＝y1+y2,

    于是△OM1M2的重心与△OM3M4的重心也重合．