B．
C．
D．
福建（文）
选择题
4．已知F1、F2是椭圆的两个焦点，过F1且与椭圆长轴垂直的直线交
椭圆于A、B两点，若△ABF2是真正三角形，则这个椭圆的离心率是
A．
B．
C． D．
6．已知m、n是不重合的直线，α、β是不重合的平面，有下列命题：
①若m
α，n∥α，则m∥n；
②若m∥α，m∥β，则α∥β；
③若α∩β=n，m∥n，则m∥α且m∥β；
④若m⊥α，m⊥β，则α∥β.
其中真命题的个数是
A．0 B．1 C．2 D．3
12．如图，B地在A地的正东方向4
km处，C
地在B地的北偏东30º方向2 km处，现要
在曲线PQ上任意选一处M建一座码头，
向B、C两地转运货物，经测算，从M到
B、C两地修建公路的费用都是a万元/km、
那么修建这两条公路的总费用最低是（ ）
A．(
+1)a万元
B．(2－2)
a万元
C．2a万元 D．(－1)
a万元
填空题
13．直线x+2y=0被曲线x2+y2－6x－2y－15=0所截得的弦长等于 .(4分)解答
解答题
21．（本小题满分12分）
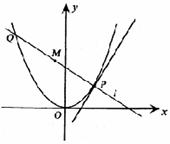
如图，P是抛物线C：y=
x2上一点，直线l过点P并与抛物线C在
点P的切线垂直，l与抛物线C相交于另一点Q.
（Ⅰ）当点P的横坐标为2时，求直线l的方程；
（Ⅱ）当点P在抛物线C上移动时，求线段PQ中点M的轨迹方程，
并求点M到x轴的最短距离.
浙江（文）
选择题
（2）直线y=2与直线x+y—2=0的夹角是
（A）
（B）
（C）
（D）
（5）点P从（1，0）出发，沿单位圆
逆时针方向运动
弧长到达Q点，
则Q的坐标为
（A）（
（B）（
（C）（
（D）（
（6）曲线y2=4x关于直线x=2对称的曲线方程是
（A）y2=8--4x （B）y2=4x—8 （C）y2=16--4x （D）y2=4x—16
（11）椭圆
的左、右焦点分别为F1、F2，线段F1F2被
点（
，0）分成5：3两段，则此椭圆的离心率为
（A）
（B）
（C）
（D）
解答题
（22）（本题满分14分）
解：已知双曲线的中心在原点，右顶点为A（1，0）点P、Q在双
曲线的右支上，支M（m,0）到直线AP的距离为1。
（Ⅰ）若直线AP的斜率为k，且
，求实数m的
取值范围；
（Ⅱ）当
时，ΔAPQ的内心恰好是点M，求此双曲
线的方程。
天津（文）
选择题
5.
设P是双曲线
上一点，双曲线的一条渐近线方程为
，
、
分别是双曲线的左、右焦点。若
，则
A. 1或5 B. 6 C. 7 D. 9
7.
若过定点
且斜率为
的直线与圆
在第一象限内的
部分有交点，则的取值范围是
A.
B.
C.
D.
8.
如图，定点A和B都在平面
内，定点
，
，C是内异于A和B的
动点，且
。那么，动点C在平面内的轨迹是
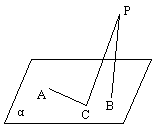
A. 一条线段，但要去掉两个点 B. 一个圆，但要去掉两个点
C. 一个椭圆，但要去掉两个点 D. 半圆，但要去掉两个点
填空题
15.
如果过两点
和
的直线与抛物线
没有交点，
那么实数
的取值范围是
。（4分）解答
解答题
22.（本小题满分14分）
椭圆的中心是原点O，它的短轴长为
，相应于焦点
的
准线
与
轴相交于点A，
，过点A的直线与椭圆相交于P、Q两点。
（1）求椭圆的方程及离心率；（2）若
，求直线PQ的方程。
江苏
选择题
5.若双曲线
的一条准线与抛物线
的准线重合，则双曲线离心率为
(A)
(B)
(C)
4 (D)
填空题
14.以点(1，2)为圆心，与直线4x+3y-35=0相切的圆的方程是_______.(4分)
解答题
21.已知椭圆的中心在原点，离心率为 EQ \F(1,2) ，一个焦点是F（-m,0）
(m是大于0的常数).
(Ⅰ)求椭圆的方程；
(Ⅱ)设Q是椭圆上的一点，且过点F、Q的直线
与y轴交于点M.
若
，
求直线的斜率.
辽宁
选择题
3．已知α、β是不同的两个平面，直线
，命题
无公共点；
命题
.
则
的
A．充分而不必要的条件 B．必要而不充分的条件
C．充要条件 D．既不充分也不必要的条件
6．已知点
、
，动点
，则点P的轨迹是
A．圆 B．椭圆 C．双曲线 D．抛物线
9．已知点
、
，动点P满足
.
当点P的纵坐标是时，
点P到坐标原点的距离是
A．
B．
C．
D．2
填空题
13．若经过点P（－1，0）的直线与圆
相切，则此直线在y轴上的截距是 .
解答题
19．（本小题满分12分）
设椭圆方程为
，过点M（0，1）的直线l交椭圆于点A、B，O是坐标原点，
点P满足
，点N的坐标为
，当l绕点M旋转时，求：
（1）动点P的轨迹方程；
（2）
的最小值与最大值.
重庆（文）
选择题
3.圆
的圆心到直线
的距离为：（ ）
A 2 B
C 1 D
10．已知双曲线
的左，右焦点分别为
,点P在双曲线
的右支上，且
,则此双曲线的离心率e的最大值为：(
)
A
B
C
D
填空题
15．已知曲线
，则过点
的切线方程是__________(4分)
解答
解答题
21．（本小题满分12分）
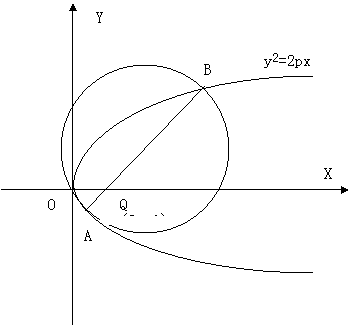
设
是一常数，过点
的直线与抛物线
交于相异
两点A、B，以线段AB为直经作圆H（H为圆心）。试证抛物线顶点
在圆H的圆周上；并求圆H的面积最小时直线AB的方程。
湖南（文）
选择题
4．如果双曲线
上一点P到右焦点的距离为
,
那么点P到右准线
的距离是（ ）
A．
B．13 C．5 D．
填空题
13．过点P（－1，2）且与曲线y=3x2-4x+2在点M（1，1）处的切线平行的
直线方程是__________.(4分) 解答
15．F1，F2是椭圆C：
的焦点，在C上满足PF1⊥PF2的点P的
个数为_______.(4分) 解答
16．若直线y=2a与函数y=|ax-1|(a>0,且a≠1)的图象有两个公共点，
则a的取值范围是_______.(4分) 解答
解答题
21．（本小题满分12分）
如图，已知曲线C1：y=x3(x≥0)与曲线C2:y=－2x3+3x(x≥0)交于O，A,
直线x=t(0<t<1)与曲线C1,C2分别交于B，D.
（Ⅰ）写出四边形ABOD的面积S与t的函数关系式S=f(t);
（Ⅱ）讨论f(t)的单调性，并求f(t) 的最大值.
22．（本小题满分14分）
如图，过抛物线x2=4y的对称轴上任一点P（0,m）(m>0)作直线与抛物线
交于A,B两点，点Q是点P关于原点的对称点。
（I）设点P分有向线段
所成的比为
，证明:
（II）设直线AB的方程是x-2y+12=0，过A,B两点的圆C与抛物线在点A处有
共同的切线，求圆C的方程.
湖北（文）
选择题
2．已知点M（6，2）和M2（1，7）.直线y=mx—7与线段M1M2的交点M分有向线段M1M2的
比为3：2，则m的值为
A．
B．
C．
D．4
4．两个圆
的公切线有且仅有
A．1条 B．2条 C．3条 D．4条
解答题
20．（本小题满分12分）
直线
的右支交于不同的两点A、B.
（Ⅰ）求实数k的取值范围；
（Ⅱ）是否存在实数k，使得以线段AB为直径的圆经过双曲线C的右焦点F？
若存在，求出k的值；若不存在，说明理由.
广东
选择题
8.
若双曲线
的焦点到它相对应的准线的距离是2，则k=
A. 6 B. 8 C. 1 D. 4
12.
如右下图,定圆半径为
( b ,c ), 则直线ax+by+c=0与直线
x–y+1=0
的交点在( )
A. 第四象限
B. 第三象限
C. 第二象限
D. 第一象限
解答题
20 (12分)某中心接到其正东、正西、正北方向三个观测点的报告：正西、
正北两个观测点同时听到了一声巨响，正东观测点听到的时间比其他两观
测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生
的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上)
22．(14分)设直线
与椭圆
相交于A、B两点，又与双曲线x2–y2=1
相交于C、D两点，
C、D三等分线段AB. 求直线的方程.
北京（文）
选择题
（3）设m、n是两条不同的直线，
是三个不同的平面，给出下列四个命题：
①若
，
，则
②若
，
，，则
③若
，，则
④若
，，则
其中正确命题的序号是
A. ①和② B. ②和③ C. ③和④ D. ①和④
填空题
（11）圆
的圆心坐标是______________，如果直线
与
该圆有公共点，那么实数a的 取值范围是______________(5分) 解答
解答题
（17）（本小题满分14分）
如图，抛物线关于x轴对称，它的顶点在坐标原点，点P（1，2），
A（），B（
）均在抛物线上。
（I）写出该抛物线的方程及其准线方程
（II）当PA与PB的斜率存在且倾斜角互补时，求
的值及直线AB的斜率
解答上海（文）
选择题
13、在下列关于直线l、m与平面α、β的命题中,真命题是( )
(A)若l
β且α⊥β,则l⊥α.
(B) 若l⊥β且α∥β,则l⊥α.
(C) 若l⊥β且α⊥β,则l∥α. (D) 若α∩β=m且l∥m,则l∥α.
填空题
2、设抛物线的顶点坐标为(2,0),准线方程为x=－1,则它的焦点
坐标为 .(4分) 解答
8、圆心在直线x=2上的圆C与y轴交于两点A(0, -4),B(0, -2),则
圆C的方程为 .(4分) 解答
11、教材中“坐标平面上的直线”与“圆锥曲线”两章内容体现出解析几何的
本质是 .(4分) 解答
解答题
20、(本题满分14分) 第1小题满分6分, 第2小题满分8分
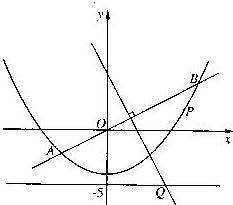如图,
直线y=
x与抛物线y=
x2－4交于A、B两点,
线段AB的垂直
平分线与直线y=－5交于Q点.
(1) 求点Q的坐标；
(2) 当P为抛物线上位于线段AB下方
(含A、B) 的动点时, 求ΔOPQ面积的最大值.
全国卷（Ⅰ）文
选择题
7．椭圆
的两个焦点为F1、F2，过F1作垂直于x轴的直线与椭圆相交，
一个交点为P，则
=
A．
B．
C． D．4
8．设抛物线y2=8x的准线与x轴交于点Q，若过点Q的直线l与抛物线有公共点，
则直线l的斜率的取值范围是
A．[－，] B．[－2，2] C．[－1，1] D．[－4，4]
填空题
15．由动点P向圆x2+y2=1引两条切线PA、PB，切点分别为A、B，∠APB=60°，
则动点P的轨迹方程为 .(4分) 解答
解答题
22．（本小题满分14分）
设双曲线C：
相交于两个不同的点A、B.
（I）求双曲线C的离心率e的取值范围：
（II）设直线l与y轴的交点为P，且
求a的值.
全国卷（Ⅱ）文
选择题
3．曲线
在点（1，－1）处的切线方程为
A．
B．
C． D．
4．已知圆C与圆
关于直线
对称，则圆C的方程为
A．
B．
C．
D．
填空题
15．设中心在原点的椭圆与双曲线
=1有公共的焦点，且它们的
离心率互为倒数，则该椭圆的方程是 .(4分)
解答题
22．（本小题满分14分）
给定抛物线C：
F是C的焦点，过点F的直线
与C相交于A、B两点.
（Ⅰ）设的斜率为1，求
夹角的大小；
（Ⅱ）设
，求在
轴上截距的变化范围.
全国卷（Ⅲ）文
选择题
5．圆
在点
处的切线方程为
A．
B．
C．
D．
8．设双曲线的焦点在
轴上，两条渐近线为
，
则该双曲线的离心率
（
）
A．
B．
C． D．
11．在△ABC中，AB=3，BC=
，AC=4，则边AC上的高为
A．
B．
C．
D．
填空题
(16) 设P为圆
上的动点，则点P到直线
的距离的最小值为
.(4分) 解答
解答题
22.（本小题满分12分）设椭圆
的两个焦点是
与
，
且椭圆上存在一点
，使得直线
与
垂直.
（1）求实数
的取值范围；
（2）设
是相应于焦点
的准线，直线与相交于点
，若
，
求直线的方程.
全国卷（Ⅳ）文
选择题
8．已知圆C的半径为2，圆心在轴的正半轴上，直线
与圆C相切，
则圆C的方程为
A．
B．
C． D．
12．△ABC中，a、b、c分别为∠A、∠B、∠C的对边.如果a、b、c成等差数列，
∠B=30°，△ABC的面积为，那么b=
A．
B．
C．
D．
解答题
19．（本小题满分12分）
已知直线
为曲线
在点（1，0）处的切线，
为该曲线
的另一条切线，且
（Ⅰ）求直线的方程；
（Ⅱ）求由直线、和轴所围成的三角形的面积.
22．（本小题满分14分）
双曲线
的焦距为2c，直线过点（a，0）和（0，b），
且点（1，0）到直线的距离与点（－1，0）到直线的距离之和
求双
曲线的离心率e的取值范围.
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。
