浙江（理）

选择题

  (3) 已知等差数列的公差为2,若成等比数列, 则=

     (A) –4      (B) –6      (C) –8    (D) –10

解答

 (7) 若展开式中存在常数项,则n的值可以是

     (A) 8    (B) 9   (C) 10    (D) 12

解答

解答题

（22）（本题满分14分）

  如图，ΔOBC的在个顶点坐标分别为（0,0）、（1,0）、（0,2）,

设P为线段BC的中点,P₂为线段CO的中点,P₃为线

段OP₁的中点,对于每一个正整数n,P_n+3为线段P_nP_n+1的

中点,令P_n的坐标为(x_n,y_n),

  （Ⅰ）求及;

（Ⅱ）证明

 (Ⅲ)若记证明是等比数列.

解答

天津（理）

选择题

8. 已知数列，那么“对任意的，点都在直线上”

是“为等差数列”的

A. 必要而不充分条件          B. 充分而不必要条件

C. 充要条件                 D. 既不充分也不必要条件

   解答

填空题

15. 若，则

          。（用数字作答）(4分)

 解答

解答题

21. （本小题满分12分）

  已知定义在R上的函数和数列满足下列条件：

  ，

，其中a为常数，k为非零常数。

（1）令，证明数列是等比数列；

（2）求数列的通项公式；

（3）当时，求。

解答

江苏

选择题

7.的展开式中x³的系数是  

(A)6     (B)12      (C)24      (D)48

解答

填空题

15.设数列{a_n}的前n项和为S_n，S_n=(对于所有n≥1)，且a₄=54，

则a₁的数值是________.

解答

解答题

20.设无穷等差数列{a_n}的前n项和为S_n.

(Ⅰ)若首项  EQ \F(3,2) ，公差，求满足的正整数k；

解答

重庆（理）

选择题

 9． 若数列是等差数列，首项，则使

前n项和成立的最大自然数n是：（     ）

     A    4005       B  4006       C    4007        D   4008

解答

填空题

13.若在的展开式中的系数为，则 解答

解答题

22．（本小题满分14分）

      设数列满足

(1)     证明对一切正整数n 成立；

(2)  令,判断的大小，并说明理由。

解答

湖南（理）

选择题

（8）数列中，则=

    （A）    （B）   （C）       （D）

解答

填空题

(15)若的展开式中的常数项为84,则n=         .(4分) 解答

解答题

（22）（本小题满分14分）

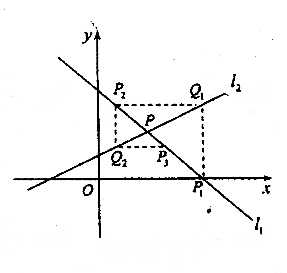
如图，直线与相交于点P。直线

与x轴交于点P₁，过点P₁作x轴的垂线交直线于点Q₁，过点Q₁作y轴的

垂线交直线于点P₂，过点P₂作x轴的垂线交直线于点Q₂，…，这样

一直作下去，可得到一系列点P₁，Q₁，P₂，Q₂，…。点P_n（n=1,2,…）

的横坐标构成数列。

  (Ⅰ)证明

(Ⅱ)求数列的通项公式；

(Ⅲ)比较与的大小。

 解答

湖北（理）

选择题

（8）已知数列{a_n}的前项和，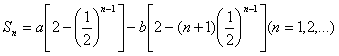

其中a、b是非零常数。则存在数列{}、{}使得

（A）a_n=+ 其中{}为等差数列，{}为等比数列

（B）a_n=+，其中{}和{}都为等差数列

（C）a_n=·，其中{}为等差数是列，{}为等比数列

（D）a_n=· 其中{}和{}都为等比数列

 解答

解答题

（22）（本小题满分14分）

已知，数列满足n=1，2，…。

A=(

（Ⅱ）设…，证明：；

（Ⅲ）若对…，都成立，求的取值范围。

 　解答

广东

解答题

17. (12分)已知成公比为2的等比数列(

也成等比数列. 求的值.

  解答

北京（理）

填空题

（14）、定义“等和数列”：在一个数列中，如果每一项与它的后一项的和

都为同一个常数，那么这个数 列叫做等和数列，这个常数叫做该数列的公和。

    已知数列是等和数列，且，公和为5，那么的值为________，

这个数列的前n项和的计算公式为___________

 解答

上海（理）

填空题

4、设等比数列{a_n}(n∈N)的公比q=－,且(a₁+a₃+a₅+…+a_2n-1)=,

则a₁=  .(4分)         解答

12、若干个能唯一确定一个数列的量称为该数列的“基本量”.设{a_n}是

公比为q的无穷等比数列,下列{a_n}的四组量中,一定能成为该数列“基本量”

的是第            组.(写出所有符合要求的组号)

     ①S₁与S₂;   ②a₂与S₃;   ③a₁与a_n;   ④q与a_n.

其中n为大于1的整数, S_n为{a_n}的前n项和.(4分)         解答

解答题

22、(本题满分18分) 第1小题满分6分, 第2小题满分4分, 第3小题满分8分

  设P₁(x₁,y₁), P₁(x₂,y₂),…, P_n(x_n,y_n)(n≥3,n∈N) 是二次曲线C上

的点, 且a₁=², a₂=², …, a_n=²构成了一个公差为d(d≠0) 的

等差数列, 其中O是坐标原点. 记S_n=a₁+a₂+…+a_n.

(1)      若C的方程为=1,n=3. 点P₁(3,0) 及S₃=255, 求点P₃的坐标；

 (只需写出一个)

(2)若C的方程为(a>b>0). 点P₁(a,0), 对于给定的自然数n, 当公

差d变化时, 求S_n的最小值；

. (3)请选定一条除椭圆外的二次曲线C及C上的一点P₁,对于给定的自然数n,

写出符合条件的点P₁, P₂,…P_n存在的充要条件,并说明理由.

 解答

全国卷（Ⅰ）理

填空题

15．已知数列{a_n}，满足a₁=1，a_n=a₁+2a₂+3a₃+…+(n－1)a_n－1(n≥2)，

                 1,n=1, 

则{a_n}的通项a_n=              ,n≥2.     (4分)  解答

解答题

22．（本小题满分14分）

已知数列，且

         a_2k=a_2k－1+(－1)^k,

           a_2k+1=a_2k+3^k,

其中k=1,2,3,…….

（I）求a₃, a₅；

（II）求{ a_n}的通项公式.

解答

全国卷（Ⅱ）理

解答题

19．（本小题满分12分）

数列的前n项和记为S_n，已知证明：

（Ⅰ）数列是等比数列；

（Ⅱ）

 解答

全国卷（Ⅲ）理

选择题

3．设数列是等差数列，且，是数列的前项和，则

      A．   B．   C．    D．

解答

解答题

22．（本小题满分14分）已知数列的前项和满足.

（1）写出数列的前三项；

（2）求数列的通项公式；

（3）证明：对任意的整数，有 .

解答

全国卷（Ⅳ）理

选择题

6．等差数列中，，则此数列

前20项和等于

       A．160       B．180       C．200       D．220

解答

填空题

13．展开式中的系数为              .(4分) 解答