福建（理）
选择题
（10）如图，A、B、C是表面积为48π的球面上三点，AB=2，BC=4，
∠ABC=60º，O为球心，则直线OA与截面ABC所成的角是
（A）arcsin
（B）arccos
（C）arcsin
（D）arccos
填空题
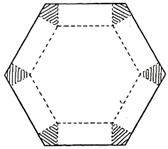（16）如图1，将边长为1的正六边形铁皮的六个角各切去一个全等的
四边形，再沿虚线折起，做成一个无 盖的正六棱柱容器。当这个正六
棱柱容器的底面边长为 时，其容积最大。
解答题
（19）（本小题满分12分）
在三棱锥S-ABC中，△ABC是边长为4的正三角形，平面SAC⊥平面ABC，
SA=SC=2
，M、N分别为AB、SB的中点。
（Ⅰ）证明：AC⊥SB；
（Ⅱ）求二面角N-CM-B的大小；
（Ⅲ）求点B到平面CMN的距离。
浙江（理）
选择题
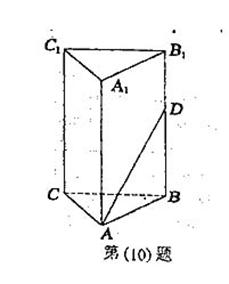
（10）如图，在正三棱柱ABC—A1B1C1中已知AB=1，D在棱BB1上，
且BD=1，若AD与平面AA1C1C所成的角为α，则α=
（A）
（B）
（C）
（D）
解答题
（19）（本题满分12分）
如图，已知正方形ABCD和矩形ACEF所在的平面互相垂直，
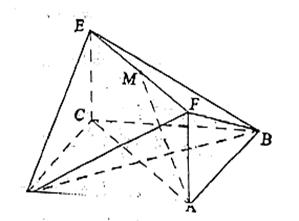AB=
，AF=1，M是线段EF的中点。
（Ⅰ）求证AM∥平面BDE；
（Ⅱ）求二面角A—DF—B的大小；
D
天津（理）
选择题
6.
如图，在棱长为2的正方体
中，O是底面ABCD的中心，E、F
分别是
、AD的中点，那么异面直线OE和
所成的角的余弦值等于
A.
B.
C.
D.
10.
如图，在长方体中，AB=6，AD=4，
。分别过BC、
的两个平行截面将长方体分成三部分，其体积分别记为
，
，
。若
，则截面
的面积为
A.
B.
C.
D.
16
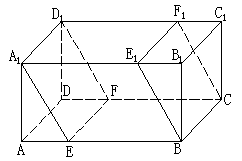
解答题
19. （本小题满分12分）
如图，在四棱锥P—ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，
PD=DC，E是PC的中点，作EF⊥PB交PB于点F。
（1）证明PA//平面EDB；
（2）证明PB⊥平面EFD；
（3）求二面角C—PB—D的大小。
江苏
选择题
4.一平面截一球得到直径是6cm的圆面，球心到这个平面的距离是4cm，
则该球的体积是
(A)
(B)
(C)
(D)
解答题
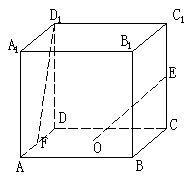
18.在棱长为4的正方体ABCD-A1B1C1D1中，O是正方形A1B1C1D1的中心，
点P在棱CC1上，且CC1=4CP.
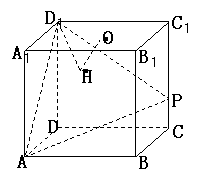(Ⅰ)求直线AP与平面BCC1B1所成的角的大小（结果用反三角函数值表示）；
(Ⅱ)设O点在平面D1AP上的射影是H，求证：D1H⊥AP；
(Ⅲ)求点P到平面ABD1的距离.
辽宁
选择题
10．设A、B、C、D是球面上的四个点，且在同一平面内，AB=BC=CD=DA=3，
球心到该平面的距离是球半径的一半，则球的体积是
A．
B．
C．
D．
填空题
15．如图，四棱柱ABCD—A1B1C1D1的底面ABCD
为正方形，侧棱与底面边长均为2a，
且
，则侧棱AA1和截面B1D1DB的距离是 .(4分)
解答题
17．（本小题满分12分）
已知四棱锥P—ABCD，底面ABCD是菱形，
平面ABCD，PD=AD，
点E为AB中点，点F为PD中点.
（1）证明平面PED⊥平面PAB；
（2）求二面角P—AB—F的平面角的余弦值.
重庆（理）
选择题
8．设P是
的二面角
内一点，
垂足，
则AB的长为：（
）
A
B
C
D
12．若三棱锥A-BCD的侧面ABC内一动点P到底面BCD的面积与到棱AB的距离
相等，则动点P的轨迹与
组成图形可能是：（
）
(C) (D)
解答题
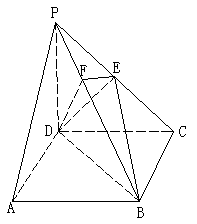
19．（本小题满分12分）
如图，四棱锥P-ABCD的底面是正方形，
(1) 证明MF是异面直线AB与PC的公垂线；
(2)
若
,求直线AC与平面EAM所成角的正弦值。
湖南（理）
选择题
(4) 把正方形ABCD沿对角线AC折起,当以A、B、C、D四点为顶点的正棱锥
体积最大时，直线BD和平面ABC所成的角的大小为
A 90 B 60 C 45 D 30
(10) 从正方体的八个顶点中任取三个点为顶点作三角形,其中直角三角形的个数为
(A)56 (B) 52 (C)48 (D)40
解答题
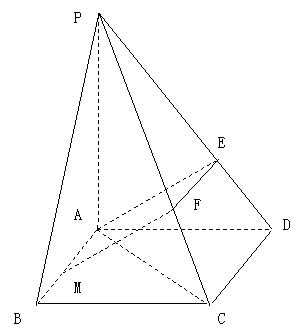
(19) (本小题满分12分)
如图,在底面是菱形的四棱锥P—ABCD中,
点E在PD上,且PE:ED= 2: 1.
(Ⅰ)证明 PA⊥平面ABCD;
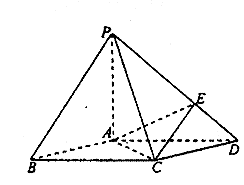(Ⅱ)求以AC为棱,EAC与DAC为面的二面角θ的大小:
(Ⅲ)在棱PC上是否存在一点F, 使BF∥平面AEC?证明你的结论.
湖北（理）
解答题
（18）（本小题满分12分）
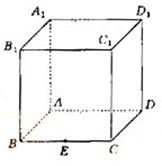如图，在棱长为1的正方体ABCD－A1、B1、C1、D1中，点E是棱BC的中点，
点F 是棱CD上的动点。
（Ⅰ）试确定点F的位置，使得D1E⊥平面AB1F；
（Ⅱ）当D1E⊥平面AB1F时，求二面角C1―EF―A的大小
（结果用反三角函数值表示）。
广东
选择题
7.在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方体,
则截去8个三棱锥后,剩下的凸多面体的体积是
A.
B.
C.
D.
填空题
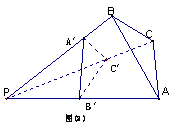
15.
由图(1)有面积关系:
则由(2)
有体积关系:
解答题
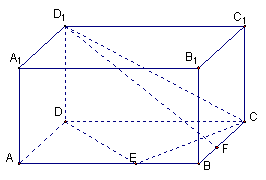
18. 如右下图,在长方体ABCD—A1B1C1D1中,已知AB= 4, AD =3, AA1= 2.
E、F分别是线段AB、BC上的点，且EB= FB=1.
(1) 求二面角C—DE—C1的正切值;
(2) 求直线EC1与FD1所成的余弦值.
北京（理）
选择题
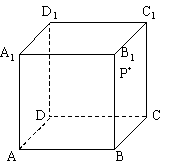
(4)、如图，在正方体
中，P是侧面
内一动点，
若P到直线BC与直线
的距离相等，则动点P的轨迹所在的曲线是
A. 直线 B. 圆 C. 双曲线 D. 抛物线
填空题
(11)、某地球仪上北纬
纬线的长度为
，该地球仪的半径是__________cm，
表面积是______________cm2（5分）
解答题
（16）（本小题满分14分）
如图，在正三棱柱
中，AB＝3，
，M为
的中点，P是BC上一点，
且由P沿棱柱侧面经
过棱
到M的最短路线长为
，设这条最短路线与的交点为N，
求：
（I）该三棱柱的侧面展开图的对角线长
（II）PC和NC的长
（III）平面NMP与平面ABC所成二面角（锐角）的大小（用反三角函数表示）
上海（理）
解答题
21、(本题满分16分) 第1小题满分4分, 第2小题满分6分, 第3小题满分6分
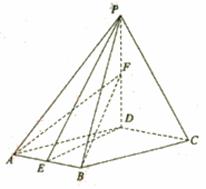
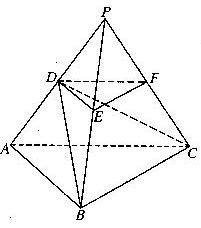如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上
的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.
(棱长和是指多面体中所有棱的长度之和)
(1) 证明：P-ABC为正四面体；
(2)
若PD=
PA,
求二面角D-BC-A的
大小；(结果用反三角函数值表示)
(3) 设棱台DEF-ABC的体积为V, 是
否存在体积为V且各棱长均相等的直
平行六面体,使得它与棱台DEF-ABC
有相同的棱长和? 若存在,请具体构造
出这样的一个直平行六面体,并给出证
明；若不存在,请说明理由.
全国卷（Ⅰ）理
选择题
10．已知正四面体ABCD的表面积为S，其四个面的中心分别为E、F、G、H.
设四面体EFGH的表面积为T，则
等于
A．
B． C． D．
填空题
16．已知a、b为不垂直的异面直线，α是一个平面，则a、b在α上的射影有可能是 .
①两条平行直线 ②两条互相垂直的直线
③同一条直线 ④一条直线及其外一点
在一面结论中，正确结论的编号是 （写出所有正确结论的编号）.
解答题
20．（本小题满分12分）
如图，已知四棱锥 P—ABCD，PB⊥AD侧面PAD为边长等于2的正三角形，
底面ABCD为菱形，侧面PAD与底面ABCD所成的二面角为120°.
（I）求点P到平面ABCD的距离，
（II）求面APB与面CPB所成二面角的大小.
全国卷（Ⅱ）理
选择题
7．已知球O的半径为1，A、B、C三点都在球面上，且每两点间的球面距离均为，
则球心O到平面ABC的距离为
A． B．
C． D．
填空题
16．下面是关于四棱柱的四个命题：
①若有两个侧面垂直于底面，则该四棱柱为直四棱柱
②若两个过相对侧棱的截面都垂直于底面，则该四棱柱为直四棱柱
③若四个侧面两两全等，则该四棱柱为直四棱柱
④若四棱柱的四条对角线两两相等，则该四棱柱为直四棱柱
其中，真命题的编号是 （写出所有正确结论的编号）.(4分)
20．（本小题满分12分）
如图，直三棱柱ABC—A1B1C1中，∠ACB=90°，AC=1，CB=
，侧棱AA1=1，侧面AA1B1B的两条对角线交点为D，B1C1的中点为M.
（Ⅰ）求证CD⊥平面BDM；
（Ⅱ）求面B1BD与面CBD所成二面角的大小.
全国卷（Ⅲ）理
选择题
9．正三棱锥的底面边长为2，侧面均为直角三角形，则此三棱锥的体积为
A．
B．
C．
D．
10．在△ABC中，AB=3，BC=
，AC=4，则边AC上的高为
A．
B．
C．
D．
填空题
13．用平面
截半径为
的球，如果球心到平面的距离为
，那么截得小圆的
面积与球的表面积的比值为 . (4分) 解答
解答题
20．（本小题满分12分）三棱锥P-ABC中，侧面PAC与底面ABC垂直，PA=PB=PC=3，
（1）求证：AB ⊥ BC；
（2）设AB=BC=，求AC与平面PBC所成角的大小. 
全国卷（Ⅳ）理
解答题
20．（本小题满分12分）
如图，四棱锥P—ABCD中，底面ABCD 为矩形，AB=8，AD=4
，侧面PAD为等边三角形，并且与底面所成二面角为60°.
（Ⅰ）求四棱锥P—ABCD的体积；
（Ⅱ）证明PA⊥BD.
本课件完全公益，使用过程中有任何问题，或想参与新课件制作，请加开心教练QQ：29443574。
