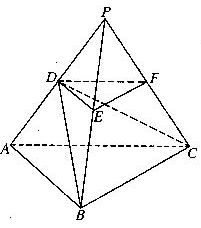
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上解答题
21、(本题满分16分) 第1小题满分4分, 第2小题满分6分, 第3小题满分6分
 如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上
如图,P-ABC是底面边长为1的正三棱锥,D、E、F分别为棱长PA、PB、PC上
的点, 截面DEF∥底面ABC, 且棱台DEF-ABC与棱锥P-ABC的棱长和相等.
(棱长和是指多面体中所有棱的长度之和)
(1) 证明:P-ABC为正四面体;
(2)
若PD=![]() PA,
求二面角D-BC-A的
PA,
求二面角D-BC-A的
大小;(结果用反三角函数值表示)
(3) 设棱台DEF-ABC的体积为V, 是
否存在体积为V且各棱长均相等的直
平行六面体,使得它与棱台DEF-ABC
有相同的棱长和? 若存在,请具体构造
出这样的一个直平行六面体,并给出证
明;若不存在,请说明理由.
【证明】(1) ∵棱台DEF-ABC与棱锥P-ABC的棱长和相等,
∴DE+EF+FD=PD+OE+PF.
又∵截面DEF∥底面ABC,
∴DE=EF=FD=PD=OE=PF,∠DPE=∠EPF=∠FPD=60°, ∴P-ABC是正四面体.
【解】(2)取BC的中点M,连拉PM,DM.AM.
∵BC⊥PM,BC⊥AM, ∴BC⊥平面PAM,BC⊥DM,
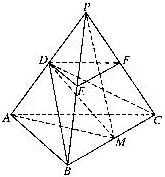 则∠DMA为二面角D-BC-A的平面角.
则∠DMA为二面角D-BC-A的平面角.
由(1)知,P-ABC的各棱长均为1,
∴PM=AM=![]() ,由D是PA的中点,得
,由D是PA的中点,得
sin∠DMA=![]() ,∴∠DMA=arcsin
,∴∠DMA=arcsin![]() .
.
(3)存在满足条件的直平行六面体.
棱台DEF-ABC的棱长和为定值6,体积为V.
设直平行六面体的棱长均为![]() ,底面相邻两边夹角为α,
,底面相邻两边夹角为α,
则该六面体棱长和为6,
体积为![]() sinα=V.
sinα=V.
∵正四面体P-ABC的体积是![]() ,∴0<V<
,∴0<V<![]() ,0<8V<1.可知α=arcsim(8V)
,0<8V<1.可知α=arcsim(8V)
故构造棱长均为![]() ,底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求.
,底面相邻两边夹角为arcsim(8V)的直平行六面体即满足要求.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。