解答题
22.(本小题满分14分)
已知数列![]() ,且
,且
a2k=a2k-1+(-1)k,
a2k+1=a2k+3k,
其中k=1,2,3,…….
(I)求a3, a5;
(II)求{ an}的通项公式.
本小题主要考查数列,等比数列的概念和基本知识,考查运算能力以及分析、
归纳和推理能力.满分14分.
解:(I)a2=a1+(-1)1=0,
a3=a2+31=3.
a4=a3+(-1)2=4,
a5=a4+32=13,
所以,a3=3,a5=13.
(II) a2k+1=a2k+3k
= a2k-1+(-1)k+3k,
所以a2k+1-a2k-1=3k+(-1)k,
同理a2k-1-a2k-3=3k-1+(-1)k-1,
……
a3-a1=3+(-1).
所以(a2k+1-a2k-1)+(a2k-1-a2k-3)+…+(a3-a1)
=(3k+3k-1+…+3)+[(-1)k+(-1)k-1+…+(-1)],
由此得a2k+1-a1=![]() (3k-1)+
(3k-1)+![]() [(-1)k-1],
[(-1)k-1],
于是a2k+1=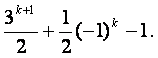
a2k= a2k-1+(-1)k
=![]() (-1)k-1-1+(-1)k
(-1)k-1-1+(-1)k
=![]() (-1)k=1.
(-1)k=1.
{an}的通项公式为:
当n为奇数时,an=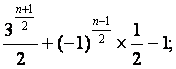
当n为偶数时,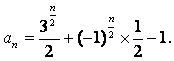
![]()
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。