解答题
19.(本小题满分12分)
设椭圆方程为![]() ,过点M(0,1)的直线l交椭圆于点A、B,O是
,过点M(0,1)的直线l交椭圆于点A、B,O是
坐标原点,点P满足![]() ,点N的坐标为
,点N的坐标为![]() ,当l绕点M旋转时,求:
,当l绕点M旋转时,求:
(1)动点P的轨迹方程;
(2)![]() 的最小值与最大值.
的最小值与最大值.
本小题主要考查平面向量的概念、直线方程的求法、椭圆的方程和性质等
基础知识,以及轨迹的求法与应用、曲线与方程的关系等解析几何的基本
思想和综合解题能力. 满分12分.
(1)解法一:直线l过点M(0,1)设其斜率为k,则l的方程为![]()
记![]() 、
、![]() 由题设可得点A、B的坐标
由题设可得点A、B的坐标![]() 、
、![]() 是方程组
是方程组
![]()
 ② 的解.………………………2分
② 的解.………………………2分
将①代入②并化简得,![]() ,所以
,所以
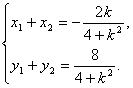 于是
于是
![]() …………6分
…………6分
设点P的坐标为![]() 则
则
 消去参数k得
消去参数k得![]() ③
③
当k不存在时,A、B中点为坐标原点(0,0),也满足方程③,所以
点P的轨迹方程为![]() ………………8分
………………8分
解法二:设点P的坐标为![]() ,因
,因![]() 、
、![]() 在椭圆上,所以
在椭圆上,所以
![]() ④
④
![]() ⑤
⑤
④—⑤得![]() ,所以
,所以
![]()
当![]() 时,有
时,有![]() ⑥
⑥
并且 ⑦
将⑦代入⑥并整理得
⑦
将⑦代入⑥并整理得
![]() ⑧
⑧
当![]() 时,点A、B的坐标为(0,2)、(0,-2),
时,点A、B的坐标为(0,2)、(0,-2),
这时点P的坐标为(0,0)也满足⑧,所以点P的轨迹方程为
 ………………8分
………………8分
(2)解:由点P的轨迹方程知![]() 所以
所以
![]() ……10分
……10分
故当![]() ,
,![]() 取得最小值,最小值为
取得最小值,最小值为![]() 时,
时,![]() 取得最大值,
取得最大值,
最大值为![]() ……………………12分
……………………12分
注:若将![]() 代入
代入![]() 的表达式求解,可参照上述标准给分.
的表达式求解,可参照上述标准给分.
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。