选择题

2.函数y=2cos²x+1(x∈R)的最小正周期为  

(A)    (B)    (C)  (D)

解答

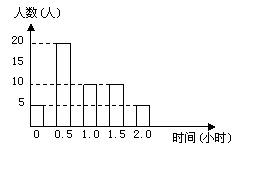
6.某校为了了解学生的课外阅读情况，随机调查了50名学生，得到他们

在某一天各自课外阅读所用时间的数据，结果用右侧的条形图表示. 根据

条形图可得这50名学生这一天平均每人的课外阅读时间为  

(A)0.6小时     (B)0.9小时      (C)1.0小时      (D)1.5小时

解答

8.若函数的图象过两点(-1，0)和(0，1)，则 

(A)a=2,b=2      (B)a=  EQ \r(,2) ,b=2       

(C)a=2,b=1      (D)a=  EQ \r(,2) ,b=  EQ \r(,2)

解答

10.函数在闭区间[-3，0]上的最大值、最小值分别是 

(A)1，-1        (B)1，-17       (C)3，-17       (D)9，-19

解答

11.设k>1，f(x)=k(x-1)(x∈R) . 在平面直角坐标系xOy中，函数y=f(x)

的图象与x轴交于A点，它的反函数y=f ^-1(x)的图象与y轴交于B点，并且这

两个函数的图象交于P点. 已知四边形OAPB的面积是3，则k等于 

(A)3     (B)  EQ \F(3,2)   (C)  EQ \F(4,3)    (D)  EQ \F(6,5)

解答

填空题

13.二次函数y=ax²+bx+c(x∈R)的部分对应值如下表：

则不等式ax²+bx+c>0的解集是__________________.(4分)

解答

解答题

19.(12分)制定投资计划时，不仅要考虑可能获得的盈利，而且要考虑可能出现的亏损.

  某投资人打算投资甲、乙两个项目. 根据预测，甲、乙项目可能的最大

盈利率分别为100﹪和50﹪，可能的最大亏损分别为30﹪和10﹪. 投资人计

划投资金额不超过10万元，要求确保可能的资金亏损不超过1.8万元. 问投

资人对甲、乙两个项目各投资多少万元，才能使可能的盈利最大？

 解答

22.(14分)已知函数满足下列条件：对任意的实数x₁，x₂都有

  和，其中是大于0的常数.

设实数a₀，a，b满足 和

(Ⅰ)证明，并且不存在，使得；

(Ⅱ)证明；

(Ⅲ)证明.

 解答