解答题

(21)(本小题满分12分)

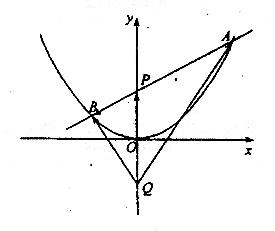
 如图,过抛物线x²=4y的对称轴上任一点P(0,m)(m>0)作直线与抛物线

交于A、B两点，点Q是点P关于原点的对称点。

  (Ⅰ)设点P分有向线段所成的比为λ，证明

(Ⅱ)设直线AB的方程是x—2y+12=0,过A、B两点的圆C与抛物线在点A处

有共同的切线，求圆C的方程。

解:

(Ⅰ)依题意,可设直线AB的方程为,代入抛物线方程得

                ①

设A、B两点的坐标分别是（x₁,y₁）、(x₂,y₂),则x₁、x₂是方程①的两根。

所以

由点P（0，m）分有向线段所成的比为，

 得， 即

又点Q是点P关于原点的以称点，

故点Q的坐标是（0，--m）,从而

          =

                =

               =

               =

               =0，

     所以

 (Ⅱ) 由得点A、B的坐标分别是（6，9）、（--4，4）。

     由得，

  所以抛物线在点A处切线的斜率为。

 设圆C的方程是，

 则

  解之得 

    所以圆C的方程是，