
解答题
18.(本小题满分12分)
如图,在棱长为1的正方体ABCD—A1B1C1D1中,AC与BD交于点E,
CB与CB1交于点F.
(I)求证:A1C⊥平BDC1;
(II)求二面角B—EF—C的大小(结果用反三角函数值表示).

本小题主要考查线面关系和正方体等基础知识,考查空间想象能力和推理能力.
满分12分.
解法一:(Ⅰ)∵A1A⊥底面ABCD,则AC是A1C在底面ABCD的射影.
∵AC⊥BD.∴A1C⊥BD.
同理A1C⊥DC1,又BD∩DC1=D,

∴A1C⊥平面BDC1.
(Ⅱ)取EF的中点H,连结BH、CH,

又E、F分别是AC、B1C的中点,

解法二:(Ⅰ)以点C为坐标原点建立如图所示的空间直角坐标系,则C(0,0,0).
D(1,0,0),B(0,1,0),A1(1,1,1),C1(0,0,1),D1(1,0,1)

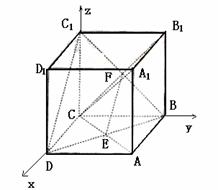
(Ⅱ)同(I)可证,BD1⊥平面AB1C.

本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。