解答题

（22）（本小题满分14分）

已知，数列满足n=1，2，…。

A=(

（Ⅱ）设…，证明：；

（Ⅲ）若对…，都成立，求的取值范围。

本小题主要考查数列、数列极限的概念和数学归纳法，考查灵活运用数学

知识分析问题和解决问题的能力，满分14分。

解：（Ⅰ）由存在，且A（A＞0），对两边取极限得，

A=，解得A=,又A＞0, ∴A=.

(Ⅱ)由得。

∴。

既对n=1,2,…都成立。

（Ⅱ）邻，得。

∴。

∴，解得。

现证明当时，，对，…都成立。

（Ⅰ）当时结论成立（已验证）。

（Ⅱ）假设当时结论成立，既，那么

。

故只须证明，既证对成立。

由于A=，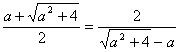

而当时，∴A≥2。

∴既

故当时， 。

既时结论成立。

根据（Ⅰ）和（Ⅱ），可知结论对一切正整数都有成立。

故对…都成立的的取值范围为。