解答题
(17)(本小题满分14分)
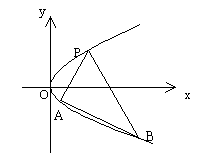
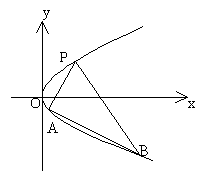
如图,过抛物线![]() 上一定点P(
上一定点P(![]() )(
)(![]() ),
),
作两条直线分别交抛物线于A(![]() ),B(
),B(![]() )
)
(I)求该抛物线上纵坐标为![]() 的点到其焦点F的距离
的点到其焦点F的距离
(II)当PA与PB的斜率存在且倾斜角互补时,
求![]() 的值,并证明直线AB的
斜率是非零常数
的值,并证明直线AB的
斜率是非零常数
本小题主要考查直线、抛物线等基本知识,考查运用解析几何的方法分析问题
和解决问题的能力。满分14分
解:(I)当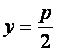 时,
时,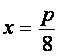
又抛物线![]() 的准线方程为
的准线方程为![]()
由抛物线定义得,所求距离为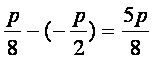
(2)设直线PA的斜率为![]() ,直线PB的斜率为
,直线PB的斜率为![]()
由![]() ,
,![]()
相减得![]()
故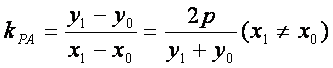
同理可得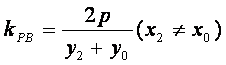
由PA,PB倾斜角互补知![]()
即
所以![]()
故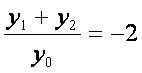
设直线AB的斜率为![]()
由![]() ,
,![]()
相减得![]()
所以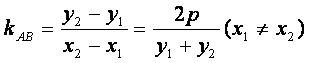
将![]() 代入得
代入得
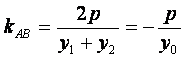 ,所以
,所以![]() 是非零常数
是非零常数
本课件完全公益,使用过程中有任何问题,或想参与新课件制作,请加开心教练QQ:29443574。